Tests concerning a population proportion
- It was claimed that 40% of human have type A blood.
- You suspect the proportion differs from 40%.
\[
\begin{aligned}
H_0:& p=0.4 \\
\\
H_a:& p \neq 0.4
\end{aligned}
\]
- Suppose \(Y\) follows a binomial distribution with
- known parameter \(n\) (number of trials)
- unknown parameter \(p\) (probability of a success)
\[
Y \sim \text{bin}(n, p)
\]
\[
\small{Y \sim \text{bin}(n, p), \;\;\;\;\text{E}[Y]=np, \;\;\;\;\text{var}(Y)=np(1-p)}
\]
\[
\small{\text{Sample proportion } \hat{P}=\frac{Y}{n} \text{ is an estimator for $p$}.}
\]
\[
\small{\text{E}\big[\hat{P}\big]=\text{E}\bigg[\frac{Y}{n}\bigg]}=\frac{1}{n}\text{E}[Y]=\frac{1}{n}np=p
\]
When the expected value of a parameter estimator is equal to the underlying parameter to be estimated, we say that the estimator is unbiased.
\[
\small{\text{var}\big(\hat{P}\big)=\text{var}\bigg(\frac{Y}{n}\bigg)}=\frac{1}{n^2}\text{var}(Y)=\frac{1}{n^2}np(1-p)=\frac{p(1-p)}{n}
\]
\[
\small{\text{When $n$ is large, the estimator }\hat{P}
\text{
is approximately } \text{N}\bigg(p, \frac{p(1-p)}{n}\bigg)}
\]
\[
\small{\text{Standardization: }\;\;\frac{\hat{P}-p}{\sqrt{\frac{p(1-p)}{n}}} \text{ is approximately } \text{N}(0, 1)}
\]
\[
\small{z=\frac{\hat{p}-p}{\sqrt{\frac{p(1-p)}{n}}}} \text{ is our test statistic.}
\]
\[
\small{H_0: p=0.4; \;\;\;\; H_a: p \neq 0.4}
\]
- A random sample of 150 donations at a blood bank reveals that 73 were type A blood.
\[
\small{
\begin{aligned}
\text{Sample proportion: }\hat{p}&=\frac{73}{150} \\
\\
\text{Test statistic: }z&=\frac{\hat{p}-p}{\sqrt{\frac{p(1-p)}{n}}}=\frac{\frac{73}{150}-0.4}{\sqrt{\frac{0.4\times0.6}{150}}}=2.167 \\
\end{aligned}
}
\]
\[
H_0: p=0.4; \;\;\;\; H_a: p \neq 0.4
\]
\[
\text{Test statistic:}\;\;z=2.167
\]
\[
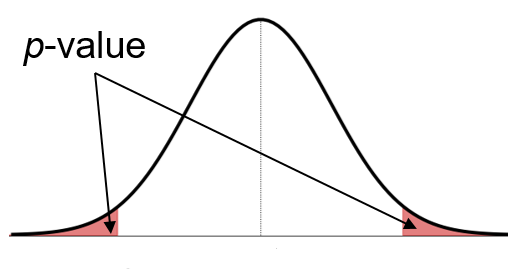
\text{$p$-value}=2\cdot\text{P}(Z>2.167) = 0.030
\]
Thus, at a significance level \(\alpha=0.05\) we reject the \(H_0\), and conclude that the proportion of type A blood differs from 40%.
- We can alsoconduct a one-tailed test for different alternative hypothesis (e.g., the proportion is higher than 40%)
\[
\small{
H_0: p=0.4; \;\;\;\; H_a: p > 0.4
}
\]
\[
\small{
\text{Test statistic:}\;\;z=2.167
}
\]
\[
\small{
\text{$p$-value}=\text{P}(Z>2.167) = 0.015
}
\]
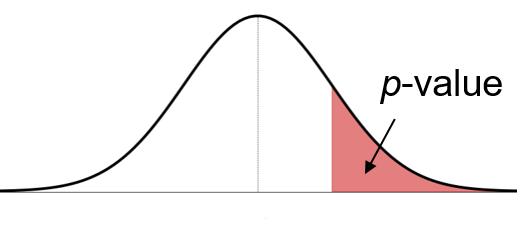
At a significance level \(\alpha=0.05\) we reject the \(H_0\)
