8.3 z-test

z-test about a population mean (upper-tailed)

Suppose \(\small{X_1, X_2, \cdots, X_n}\) are i.i.d. normal, with unknown mean \(\mu\) and known variance \(\sigma^2=100\).

\[ \small{H_0: \mu=40, \;\;\;\;H_a: \mu > 40} \]

\[ n=25, \;\; \small{\bar{x}=42},\;\; \bar{X} \sim \text{N}\big(\mu, \frac{100}{25}\big) \]

\[ \small{p\text{-value}=\text{P}\big(\bar{X}\geq 42 \text{ $\mid$ $H_0$ is true}\big)} \]

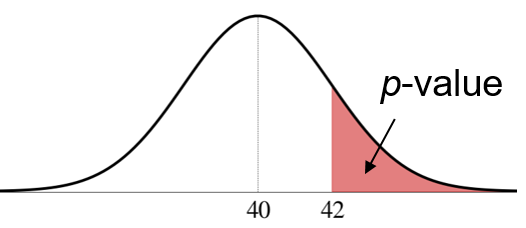
\[ \small{ \begin{aligned} p\text{-value}&=\text{P}\big(\bar{X}\geq 42 \text{ $\mid$ $H_0$ is true}\big) \\ &=\text{P}\big(\bar{X}\geq 42 \text{ $\mid$ $\mu=40$ } \big) \\ &=\text{P}\bigg(\frac{\bar{X}-40}{2} \geq \frac{42-40}{2}\bigg) \\ &=\text{P}(Z \geq 1) \\ &=0.1587 \\ \end{aligned} } \]

\[ \small{\text{At $\alpha=0.05$ we fail to reject $H_0$ as the $p$-value exceeds $\alpha$.}} \]

An alterative method

\[ \small{\text{Test statistic: }\;\;z=\frac{\bar{x}-\mu}{\sigma/\sqrt{n}}}=\frac{42-40}{2}=1 \]

\[ \small{\text{At } \alpha=0.05 \text{ the critical value } z_{\alpha}=1.645} \]

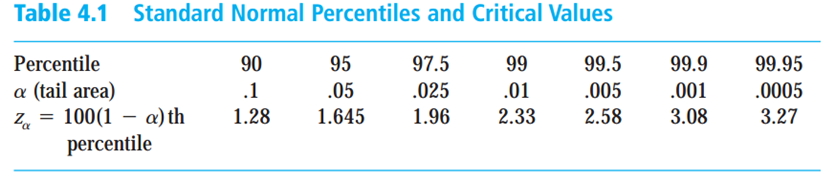
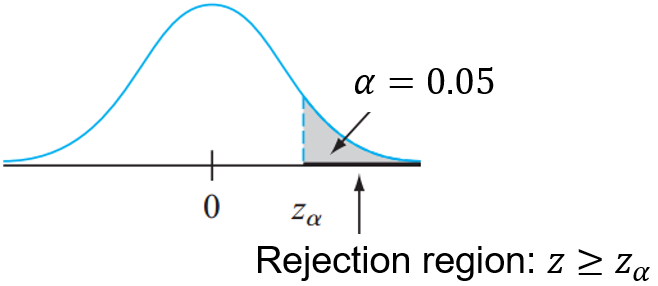
\[ \small{\text{Since the test statistic } z < z_{\alpha}, \text{we failed to reject $H_0$.}} \]

z-test about a population mean (lower-tailed)

Suppose \(X_1, X_2, \cdots, X_n\) are i.i.d. normal, with unknown mean \(\mu\) and known variance \(\sigma^2=100\).

\[ \small{H_0: \mu=40, \;\;\;\;H_a: \mu < 40} \]

\[ \small{n=25, \;\; \bar{x}=36, \;\; \bar{X} \sim \text{N}\big(\mu, \frac{100}{25}\big)} \]

\[ \small{p\text{-value}=\text{P}(\bar{X}\leq 36 \mid H_0 \text{ is true})} \]

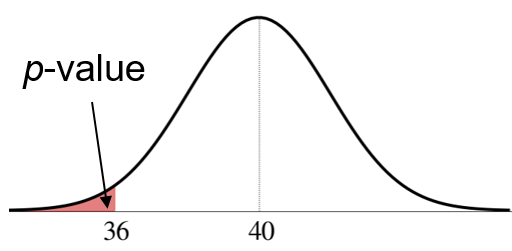
\[ \small{ \begin{aligned} p\text{-value}&=\text{P}(\bar{X} \leq 36 \text{ $\mid$ $H_0$ is true}) \\ &=\text{P}(\bar{X}\leq 36 \mid \mu=40 ) \\ &=\text{P}\bigg(\frac{\bar{X}-40}{2} \leq \frac{36-40}{2}\bigg) \\ &=\text{P}(Z \leq -2) = 0.0228 \\ \end{aligned} } \]

\[ \small{\text{At $\alpha=0.05$ we reject $H_0$ as the $p$-value is smaller than $\alpha$.}} \]

Similarly, we can also use the test statistic.

\[ \small{\text{Test statistic: }\;\;z=\frac{\bar{x}-\mu}{\sigma/\sqrt{n}}}=\frac{36-40}{2}=-2 \]

\[ \small{\text{At } \alpha=0.05 \text{ the critical value } z_{\alpha}=1.645} \]

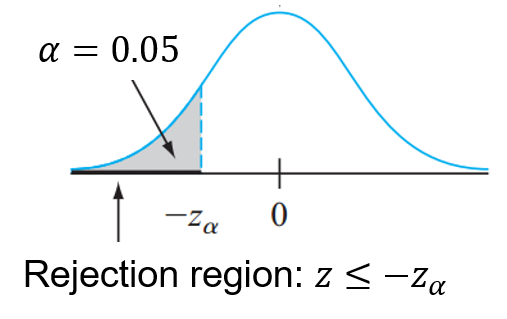
\[ \small{\text{Since the test statistic $z< -z_{\alpha}$, we reject $H_0$.}} \]

z-test about a population mean (two-tailed)

Suppose \(X_1, X_2, \cdots, X_n\) are i.i.d. normal, with unknown mean \(\mu\) and known variance \(\sigma^2=100\).

\[ \small{H_0: \mu=40, \;\;\;\;H_a: \mu \neq 40} \]

\[ \small{n=25, \;\; \bar{x}=36, \;\; \bar{X} \sim \text{N}\big(\mu, \frac{100}{25}\big)} \]

\[ \small{\text{$p$-value}=\text{P}\big(\bar{X}\leq 36 \text{ or } \bar{X}\geq 44 \text{ $\mid$ $H_0$ is true}\big)} \]

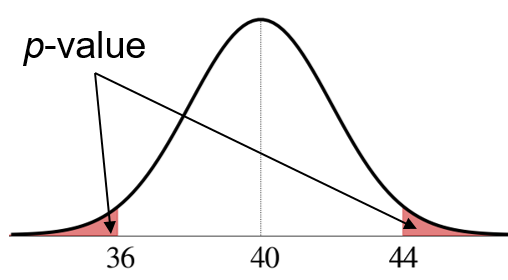
\[ \small{ \begin{aligned} \text{$p$-value}&=\text{P}\big(\bar{X}\leq 36 \text{ or } \bar{X}\geq 44 \text{ $\mid$ $H_0$ is true}\big) \\ \\ &=2\cdot \text{P}(\bar{X}\leq 36 \mid \mu=40) \\ \\ &=2\cdot \text{P}\bigg(\frac{\bar{X}-40}{2} \leq \frac{36-40}{2}\bigg) \\ \\ &=2\cdot \text{P}(Z \leq -2) = 0.0456 \\ \end{aligned} } \]

\[ \small{\text{At $\alpha=0.05$ we reject $H_0$ as the $p$-value is smaller than $\alpha$.}} \]

Similarly, we can also use the test statistic.

\[ \small{\text{Test statistic: }\;\;z=\frac{\bar{x}-\mu}{\sigma/\sqrt{n}}}=\frac{36-40}{2}=-2 \]

\[ \small{\text{At } \alpha=0.05 \text{ the critical value } z_{\alpha/2}=1.96} \]

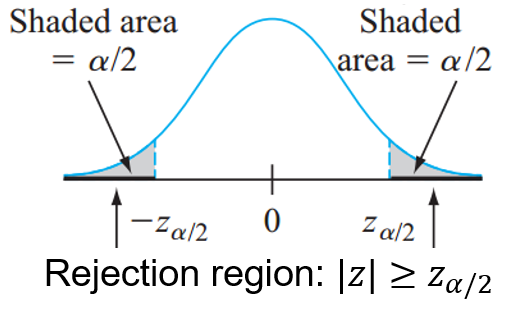
\[ \small{\text{Since $|z|> z_{\alpha/2}$, we reject $H_0$.}} \]

Large-sample tests

Recall the large-sample confidence interval.

If the sample size \(n\) is sufficiently large,

\[ \frac{\bar{X}-\mu}{\hat{S}_n/\sqrt{n}} \]

has approximately a standard normal distribution.

• We can use \(\hat{S}_n\) to replace \(\sigma\).
• Then follow the exact same z-test procedure as before.
• Rule of thumb for sample size: \(n > 40\).