7.2 Confidence interval
Point estimate
- Based on 80 samples, the battery life is \(\hat{\theta}=11.4\) hours.
- It provides no info about how precise the estimate is.
- Oftentimes, we are interested in constructing a so-called confidence interval (CI).
- Roughly speaking, it is an interval that contains the parameter with a specified high probability (e.g., 95%).
- The battery life has a 95% CI of [10.2,12.7] hours.
Constructing a confidence interval
- First, we need to specify a desired high probability.
- This high probability is called the confidence level.
- Common choices include 95% and 99%
- \((1-\alpha)\) is often used to indicate the confidence level
\[95\% \; \rightarrow \alpha=0.05\]
\[99\% \; \rightarrow \alpha=0.01\]
Constructing a confidence interval
- Once we specified the confidence level, say 95%, we aim to have a confidence interval with
- a lower bound estimator \(\hat{\Theta}_n^{-}\)
- an upper bound estimator \(\hat{\Theta}_n^{+}\)
- so that
\[\text{P}\bigg(\hat{\Theta}_n^{-} \leq \theta \leq \hat{\Theta}_n^{+}\bigg) = 95\%\]
Procedures for constructing a CI
Suppose \(X_1, X_2, \cdots, X_n\) are i.i.d. normal, with unknown mean \(\theta\) and a known variance1 \(\sigma^2\).
\[ \hat{\Theta}_n=\frac{X_1+X_2+\cdots+X_n}{n} \]
\[ \hat{\Theta}_n \sim \text{N}\bigg(\theta, \frac{\sigma^2}{n}\bigg)\;\;\rightarrow\;\;\frac{\hat{\Theta}_n-\theta}{\sigma/\sqrt{n}} \sim \text{N}(0, 1) \]
Procedures for constructing a CI
Let’s construct a 95% CI, that is, \(\alpha=0.05\).
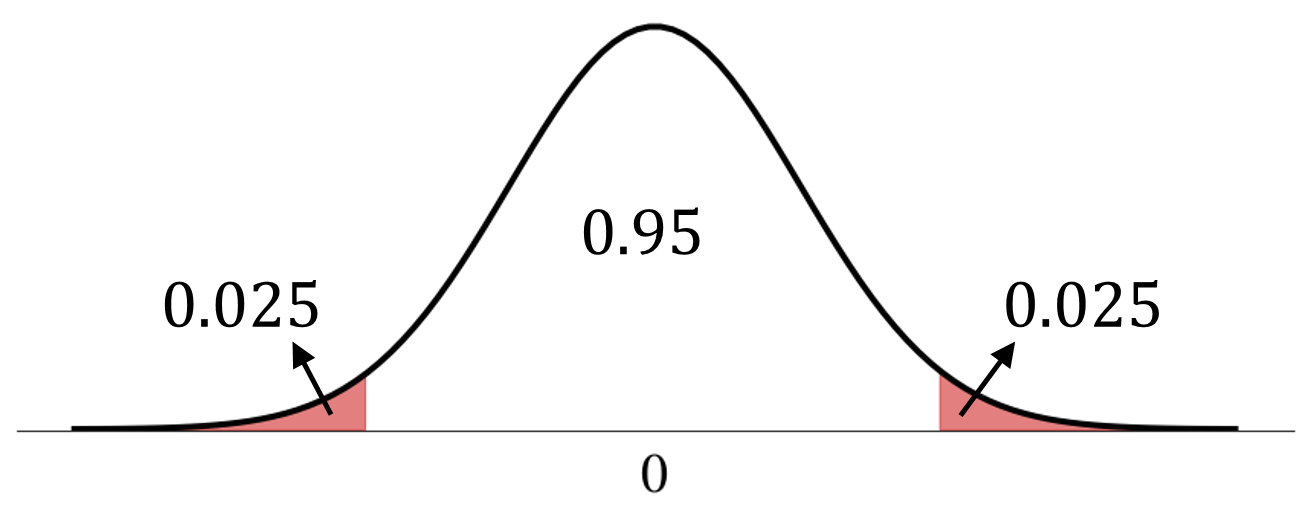
\[ \begin{aligned} \Phi(\color{red}{?})&=0.025 \\ \Phi(\color{red}{?})&=1-0.025=0.975 \\ \end{aligned} \]
It is called a critical value of \(z\) corresponding to \(0.025\).
We can check the standard normal table (next slide).
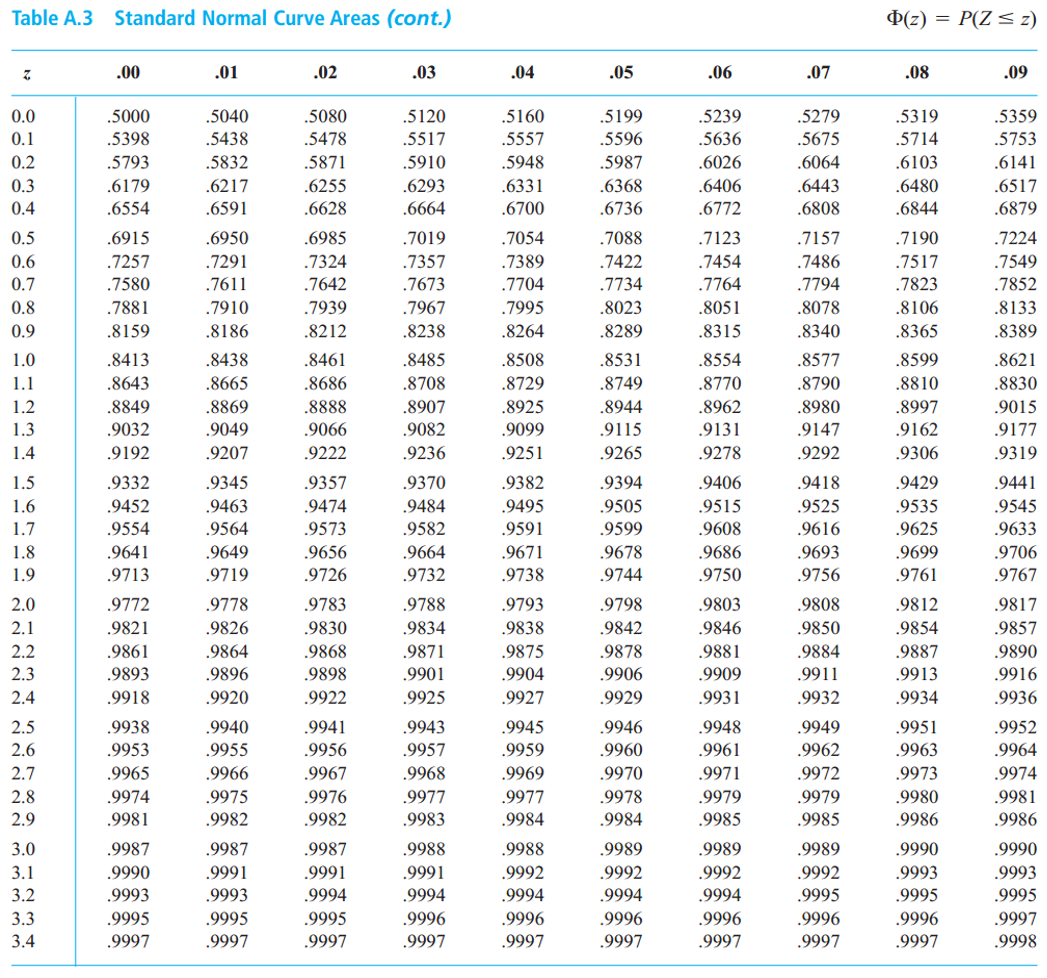
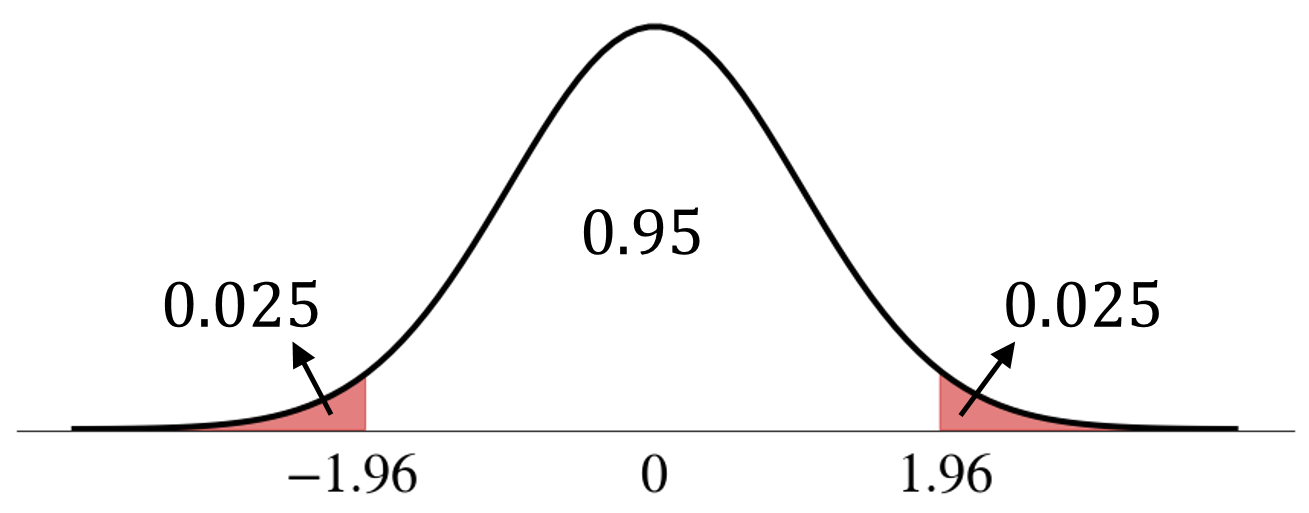
We want
\[ \text{P}\bigg(-1.96 < \frac{\hat{\Theta}_n-\theta}{\sigma/\sqrt{n}} < 1.96\bigg) = 0.95 \]
Multiply through by \(\sigma/\sqrt{n}\)
\[ \small{ \text{P}\bigg(-1.96 \cdot \frac{\sigma}{\sqrt{n}} < \hat{\Theta}_n-\theta < 1.96 \cdot \frac{\sigma}{\sqrt{n}}\bigg) = 0.95 } \]
Subtract \(\hat{\Theta}_n\) from each term
\[ \small{ \text{P}\bigg(-\hat{\Theta}_n-1.96 \cdot \frac{\sigma}{\sqrt{n}} < -\theta < -\hat{\Theta}_n + 1.96 \cdot \frac{\sigma}{\sqrt{n}}\bigg) = 0.95 } \]
Multiply through by \(-1\)
\[ \small{ \text{P}\bigg(\hat{\Theta}_n + 1.96 \cdot \frac{\sigma}{\sqrt{n}} > \theta > \hat{\Theta}_n - 1.96 \cdot \frac{\sigma}{\sqrt{n}}\bigg) = 0.95 } \]
Rearange the sides.
\[ \text{P}\bigg(\hat{\Theta}_n - 1.96 \cdot \frac{\sigma}{\sqrt{n}} < \theta < \hat{\Theta}_n + 1.96 \cdot \frac{\sigma}{\sqrt{n}}\bigg) = 0.95 \]
This means that
\[ \bigg[\hat{\Theta}_n - 1.96 \cdot \frac{\sigma}{\sqrt{n}},\;\; \hat{\Theta}_n + 1.96 \cdot \frac{\sigma}{\sqrt{n}}\bigg] \]
is a 95% confidence interval.
More compactly, it can be written as \(\hat{\Theta}_n \pm 1.96 \cdot \frac{\sigma}{\sqrt{n}}\)
More generally, for a confidence level of \(1-\alpha\),
let \(z_{\frac{\alpha}{2}}\) be such that \(\Phi(z_{\frac{\alpha}{2}})=1-\frac{\alpha}{2}\).
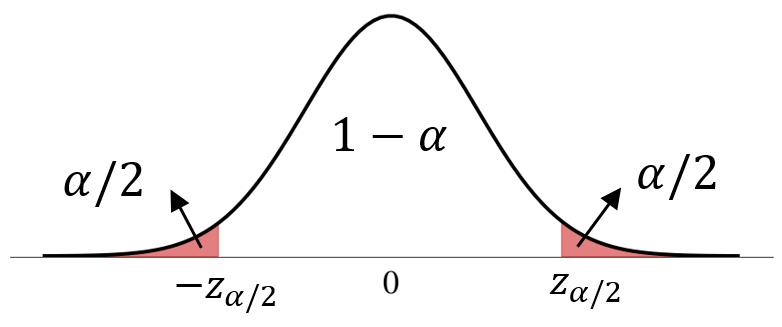
\[ \small{ \text{P}\bigg(\hat{\Theta}_n - z_{\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}} < \theta < \hat{\Theta}_n + z_{\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}}\bigg) = 1-\alpha } \]
\[ \small{ \bigg[\hat{\Theta}_n - z_{\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}},\;\; \hat{\Theta}_n + z_{\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}}\bigg]}, \;\;\text{or }\;\; \hat{\Theta}_n \pm z_{\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n} } \]
is a \((1-\alpha)\) confidence interval.
Interpretation
- Assume we have calculated the 95% confidence interval for an unknown parameter \(\theta\) as \([10.21,12.69]\).
- What does this interval mean?
- Does it mean that the true parameter \(\theta\) lies in this CI \([10.21,12.69]\) with a probability of 95%?
- No. \(\theta\) is a unknown but fixed parameter. The CI that we obtained \([10.21,12.69]\) is a fixed interval.
- We construct a CI many times w/ the same procedure.
- That is, each time we
- obtain an independent collection of \(n\) observations
- construct a 95% CI based on the \(n\) observations
- We expect that about 95% of these CIs will include \(\theta\).
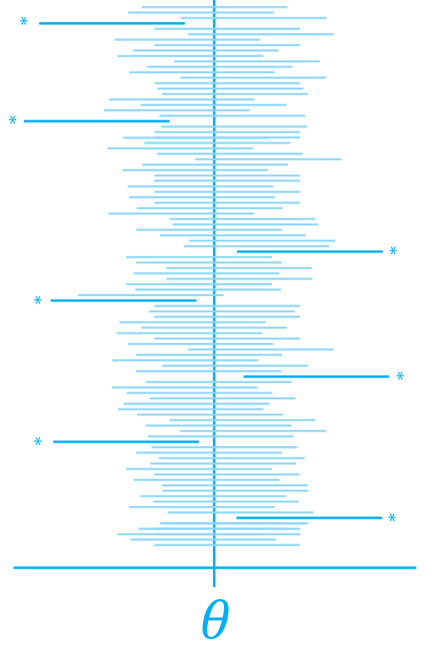
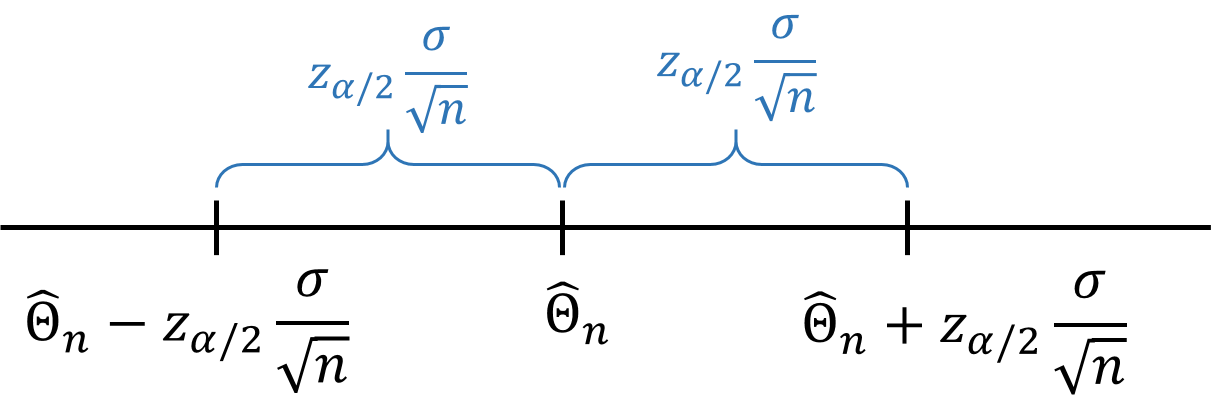
- It is a random interval centered at point estimate \(\hat{\Theta}_n\).
- The half-width of the CI is \(z_{\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}}\).
- The width of the CI indicates how precise the estimate is.
\[ \hat{\Theta}_n \pm z_{\alpha/2} \frac{\sigma}{\sqrt{n}} \]

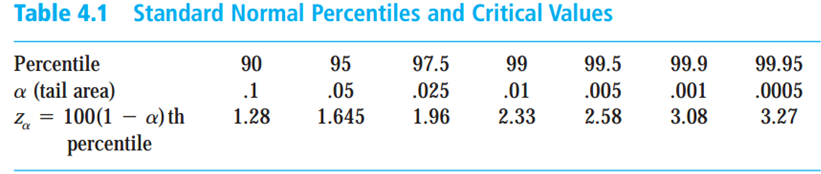
\[ \text{90% CI: }\;\;\;\; \hat{\Theta}_n \pm 1.645 \frac{\sigma}{\sqrt{n}} \]
\[ \text{95% CI: }\;\;\;\; \hat{\Theta}_n \pm 1.96 \frac{\sigma}{\sqrt{n}} \]
\[ \text{99% CI: }\;\;\;\; \hat{\Theta}_n \pm 2.58 \frac{\sigma}{\sqrt{n}} \]
\[ \hat{\Theta}_n \pm z_{\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}} \]
The half-width is proportional to \(\sigma\) (population standard deviation), the inherent variability of the thing we are trying to measure.
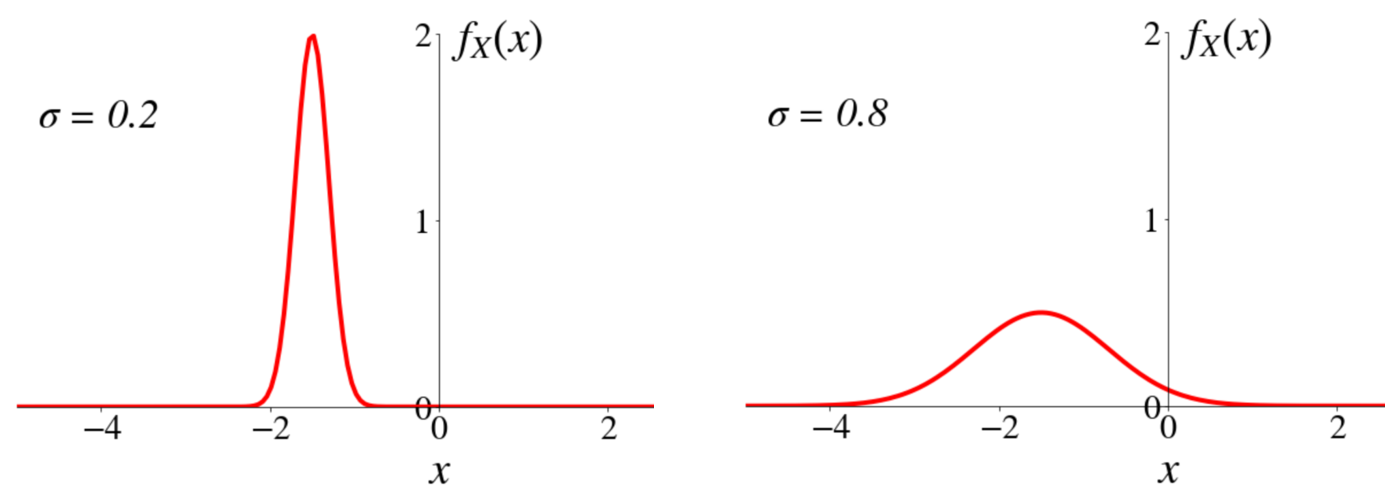
\[ \hat{\Theta}_n \pm z_{\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}} \]
The half-width decreases as sample size \(n\) increases.
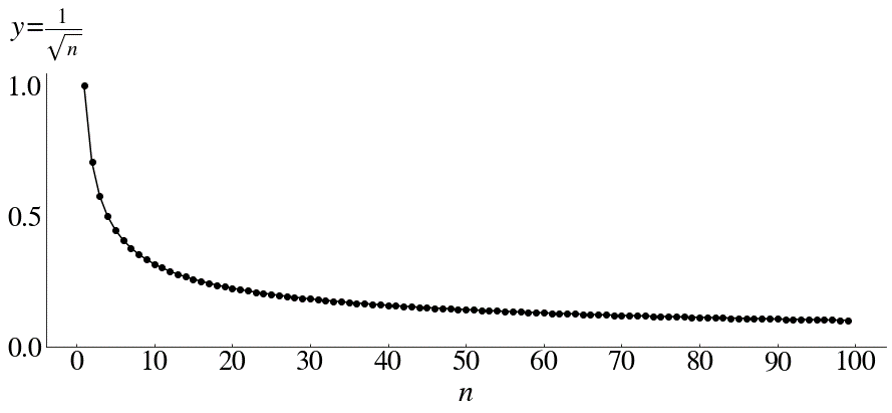
Sample size calculation
- We often have a desired precision (i.e., \(\pm 0.5\) hours) and a confidence level (e.g., 99%) for a confidence interval.
- Question: how many data points should we collect?
\[ \text{Half width:}\;\;d=z_{\frac{\alpha}{2}} \cdot \frac{\sigma}{\sqrt{n}}, \;\;\;\;\text{Solve for $n$.} \]
The sample size needed for a desired half-width of \(d\) is
\[ n=\bigg(z_{\frac{\alpha}{2}} \cdot \frac{\sigma}{d}\bigg)^2 \]
Suppose \(X_1, X_2, \cdots, X_n\) are i.i.d. normal, with unknown mean \(\theta\) and known variance \(\sigma^2\).
\[ \small{ \text{Sample mean estimator:}\;\;\hat{\Theta}_n=\frac{X_1+X_2+\cdots+X_n}{n} } \]
\[ \small{ \text{var}\big(\hat{\Theta}_n\big)=\frac{\sigma^2}{n}, \;\;\;\;\sqrt{\text{var}\big(\hat{\Theta}_n\big)}=\frac{\sigma}{\sqrt{n}} } \]
The standard deviation of \(\hat{\Theta}_n\) is termed standard error.
\[ \hat{\Theta}_n \pm z_{\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}} \]
The CI above can be expressed in words as
\[ \text{(point estimate)} \pm \text{($z$ critical value}) \cdot \text{(standard error)} \]
Suppose \(X_1, X_2, \cdots, X_n\) are
- i.i.d. (not necessarily follow a normal distribution)
- with unknown mean \(\theta\) and known variance \(\sigma^2\)
\[ \small{\text{Sample mean estimator:}\;\;\hat{\Theta}_n=\frac{X_1+X_2+\cdots+X_n}{n}} \]
If \(n\) is sufficiently large, what does the CLT tell us?
\[ \small{ \begin{aligned} \hat{\Theta}_n \;&\text{ is approximately } \text{N}\bigg(\theta, \frac{\sigma^2}{n}\bigg) \\ \frac{\hat{\Theta}_n-\theta}{\sigma/\sqrt{n}} \;&\text{ is approximately } \text{N}(0, 1) \\ \end{aligned} } \]
Procedures for constructing a CI
We can proceed exactly as in the previous case.

\[ \text{P}\bigg(-z_{\frac{\alpha}{2}} < \frac{\hat{\Theta}_n-\theta}{\sigma/\sqrt{n}} < z_{\frac{\alpha}{2}}\bigg) \approx 1-\alpha \;\;\;\color{gray}{\rightarrow \text{by CLT}} \]
\[ \text{P}\bigg(\hat{\Theta}_n - z_{\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}} < \theta < \hat{\Theta}_n + z_{\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}}\bigg) \approx 1-\alpha \]
What if we don’t know \(\sigma^2\)?
Suppose \(X_1, X_2, \cdots, X_n\) are i.i.d. with unknown mean \(\theta\) and unknown variance \(\sigma^2\).
\[ \small{ \text{Sample mean estimator:}\;\;\hat{\Theta}_n=\frac{X_1+X_2+\cdots+X_n}{n} } \]
We can estimate the population variance \(\sigma^2\) with
\[ \small{ \text{Sample variance estimator:}\;\;\hat{S}_n^2=\frac{\sum\big(X_i - \hat{\Theta}_n\big)^2}{n-1} } \]
\[ \small{ \frac{\hat{\Theta}_n-\theta}{\sigma/\sqrt{n}} \sim \text{N}(0, 1), \; \text{if $X_i$ is normally distributed.} } \]
\[ \small{ \frac{\hat{\Theta}_n-\theta}{\sigma/\sqrt{n}} \text{ is approximately } \text{N}(0, 1), \; \text{if $X_i$ is not normal, but $n$ is large.} } \]
Once we replace \(\sigma\) with \(\hat{S}_n\), we have
\[ \small{ \frac{\hat{\Theta}_n-\theta}{\hat{S}_n/\sqrt{n}} } \]
\[ \small{ \frac{\hat{\Theta}_n-\theta}{\hat{S}_n/\sqrt{n}} \text{ is approximately } \text{N}(0, 1), \; \text{if $n$ is sufficiently large.} } \]
If \(n\) is sufficiently large,
\[ \small{ \text{P}\bigg(-z_{\frac{\alpha}{2}} < \frac{\hat{\Theta}_n-\theta}{\hat{S}_n/\sqrt{n}} < z_{\frac{\alpha}{2}}\bigg) \approx 1-\alpha } \]
Generally speaking, \(n>40\) would be sufficient.
\[ \small{ \hat{\Theta}_n \pm z_{\frac{\alpha}{2}} \frac{\hat{S}_n}{\sqrt{n}} } \]
is a CI for \(\theta\) with confidence level approximately \(1-\alpha\).
\[ \small{ \text{(point estimate)} \pm \text{($z$ critical value)} \cdot \text{(estimated standard error)} } \]
What if the sample size \(n\) is small?
Suppose \(X_1, X_2, \cdots, X_n\) are i.i.d. normal with unknown mean \(\theta\) and unknown variance \(\sigma^2\).
\[ \small{ \text{Sample mean estimator:}\;\;\hat{\Theta}_n=\frac{X_1+X_2+\cdots+X_n}{n} } \]
\[ \small{ T_n=\frac{\hat{\Theta}_n-\theta}{\hat{S}_n/\sqrt{n}} } \]
has a probability distribution called a t-distribution with \(v=n-1\) degrees of freedom.
\[ \small{ t\text{-distribution:}\;\;\;T_n=\frac{\hat{\Theta}_n-\theta}{\hat{S}_n/\sqrt{n}} } \]
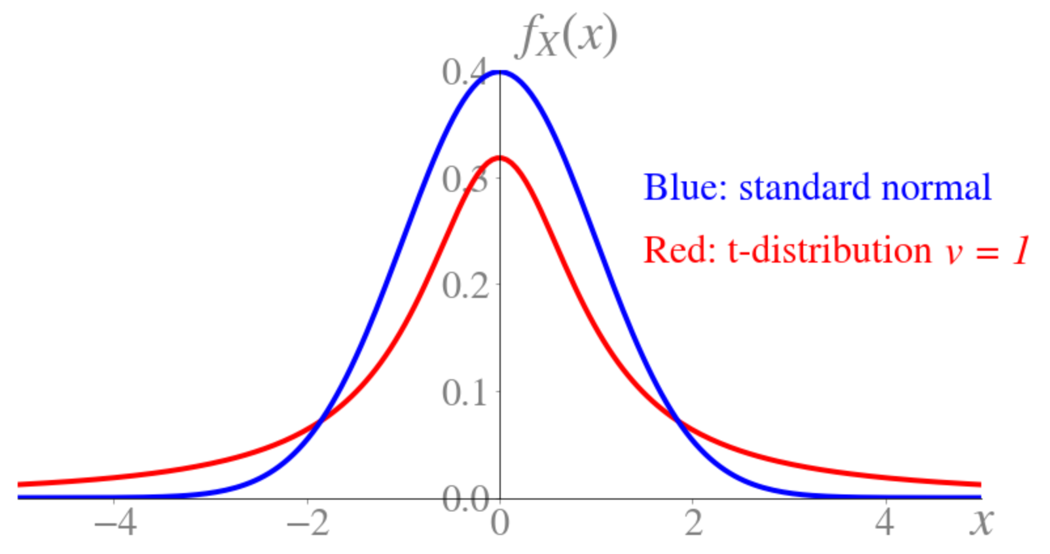
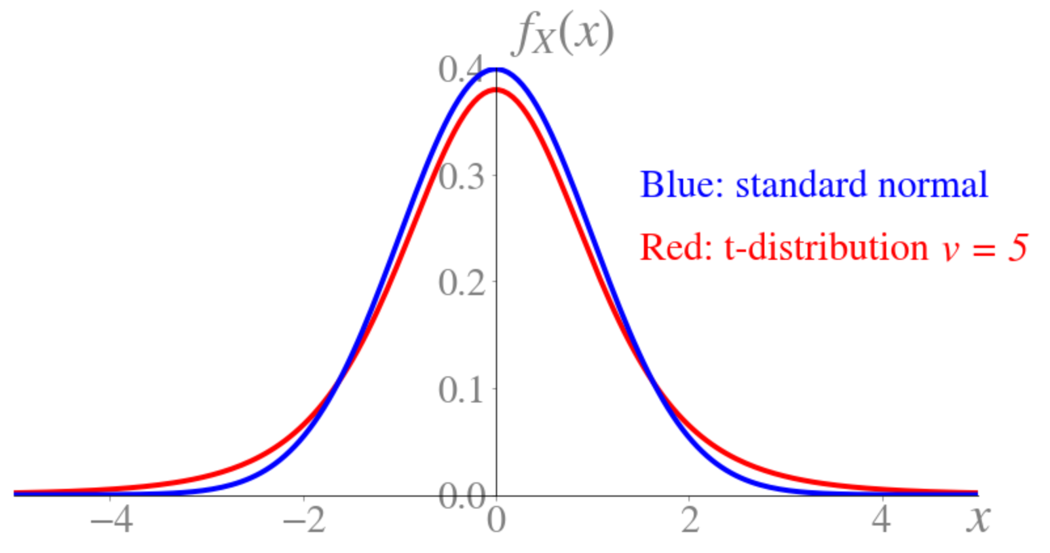
t-distribution
- Symmetric
- Bell-shaped
- More spread out than \(N(0, 1)\)
- Approaches \(N(0, 1)\) as \(v\rightarrow +\infty\)
Interactive visualization
For small \(n\), we use t-distribution to construct the CI.
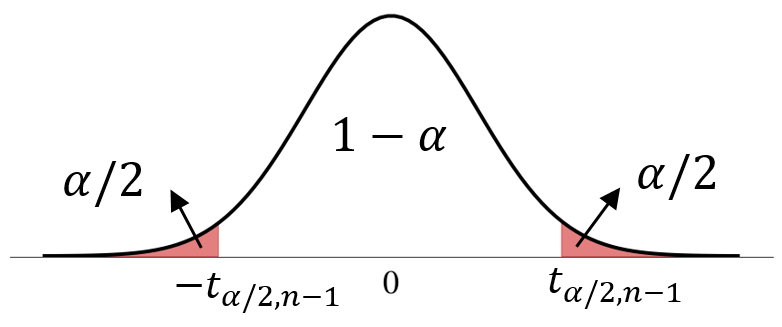
\[ \small{ \text{P}\bigg(-t_{\frac{\alpha}{2}, n-1} < \frac{\hat{\Theta}_n-\theta}{\hat{S}_n/\sqrt{n}} < t_{\frac{\alpha}{2}, n-1}\bigg) = 1-\alpha } \]
\[ \small{ \text{P}\bigg(\hat{\Theta}_n - t_{\frac{\alpha}{2}, n-1} \frac{\hat{S}_n}{\sqrt{n}} < \theta < \hat{\Theta}_n + t_{\frac{\alpha}{2}, n-1} \frac{\hat{S}_n}{\sqrt{n}}\bigg) \approx 1-\alpha } \]
\[ \small{ \text{Or, more compactly, }\hat{\Theta}_n \pm t_{\frac{\alpha}{2}, n-1} \frac{\hat{S}_n}{\sqrt{n}}\;\;\text{is a } (1-\alpha) \text{ CI.} } \]
Critical values for t-distribution
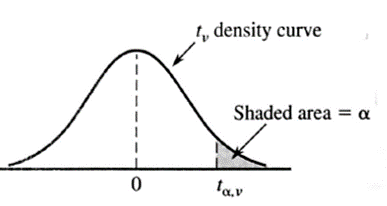
Table in next slide.
Exercise
An object is weighted using a scale.
The scale reports the true weight plus a random error that is normal with \(\mu=0\) and unknown variance.
Assume that the errors are independent.
The object was weighted eight times.
\[[0.555, 0.540, 0.636, 0.644, 0.492, 0.567, 0.556, 0.607]\]
Construct a 95% confidence interval for the weight.
\[ \small{ \bigg[\hat{\Theta}_n - t_{\frac{\alpha}{2}, n-1} \frac{\hat{S}_n}{\sqrt{n}}, \;\;\;\hat{\Theta}_n + t_{\frac{\alpha}{2}, n-1} \frac{\hat{S}_n}{\sqrt{n}}\bigg] } \]
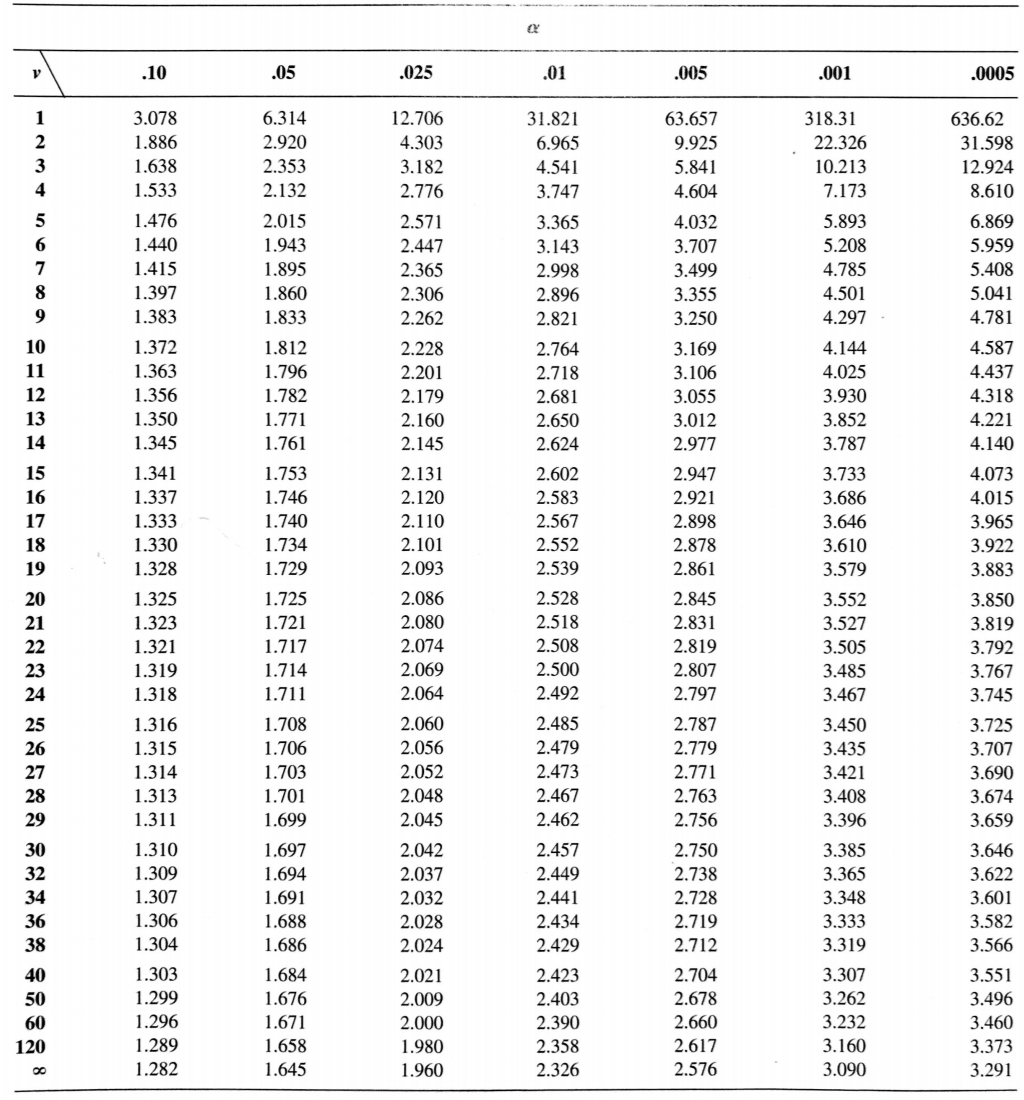
\[ \small{ \begin{aligned} \text{Sample mean:}&\; \hat{\Theta}_n=\frac{1}{n}\sum_{i=1}^n X_i=0.5746 \\ \text{Sample variance:}&\; \hat{S}_n^2=\frac{1}{n-1}\sum_{i=1}^n \big(X_i - \hat{\Theta}_n\big)^2=0.002635 \\ \text{Critical value:}&\; t_{\frac{\alpha}{2}, n-1}=t_{0.025, 7}=2.365 \\ \end{aligned} } \]
\[ \small{ \bigg[\hat{\Theta}_n - t_{\frac{\alpha}{2} n-1} \frac{\hat{S}_n}{\sqrt{n}}, \hat{\Theta}_n + t_{\frac{\alpha}{2}, n-1} \frac{\hat{S}_n}{\sqrt{n}}\bigg]=[0.532, 0.618] } \]