6.3 Central limit theorem
Let \(X_1, X_2, \cdots, X_n\) be i.i.d. with \(\mu\) and \(\sigma^2\).
\[
\small{
\begin{aligned}
\bar{X}_n&=\frac{X_1+X_2+\cdots+X_n}{n} \\
\\
S_n&=X_1+X_2+\cdots+X_n \\
\end{aligned}
}
\]
Then, if \(n\) is large,
\[
\begin{aligned}
&\bar{X}_n \text{ is approximately } \text{N}(\mu, \frac{\sigma^2}{n}) \\
&S_n \text{ is approximately } \text{N}(n\mu, n\sigma^2) \\
\end{aligned}
\]
\[
\begin{aligned}
&\bar{X}_n \text{ is approximately } \text{N}(\mu, \frac{\sigma^2}{n}) \\
&S_n \text{ is approximately } \text{N}(n\mu, n\sigma^2) \\
\end{aligned}
\]
Their standardized version: \[
\begin{aligned}
\frac{\bar{X}_n-\mu}{\sigma/\sqrt{n}} &\text{ is approximately } \text{N}(0, 1) \\
\\
\frac{S_n-n\mu}{\sqrt{n}\sigma} &\text{ is approximately } \text{N}(0, 1) \\
\end{aligned}
\]
\[
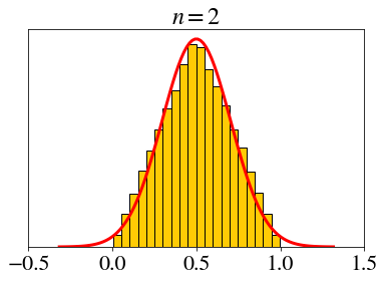
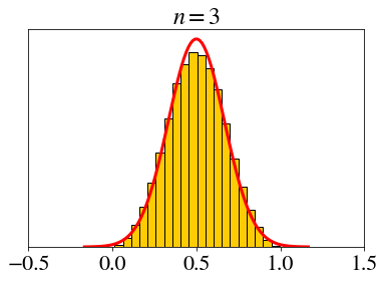
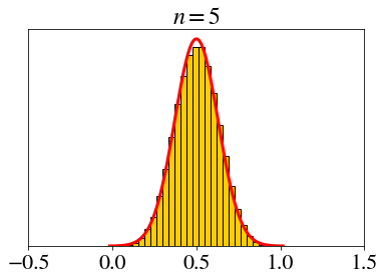
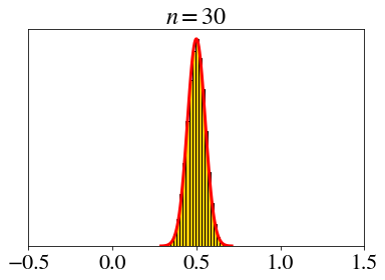
X_i \sim \text{unif}(0, 1),\;\; \bar{X}_n=\frac{X_1+X_2+\cdots+X_n}{n}
\]
\[
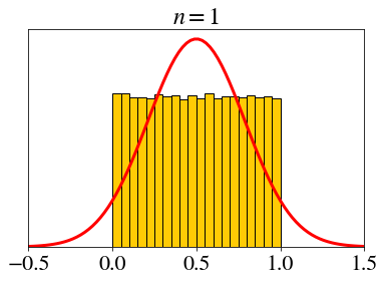
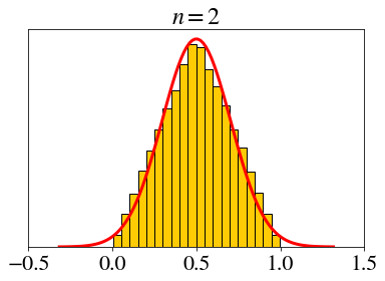
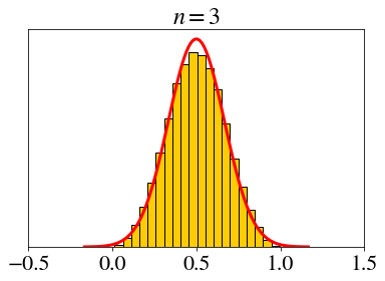
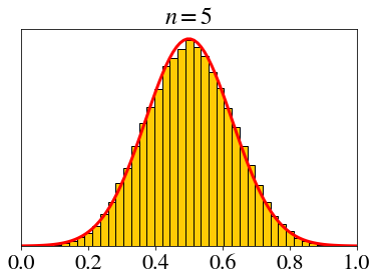
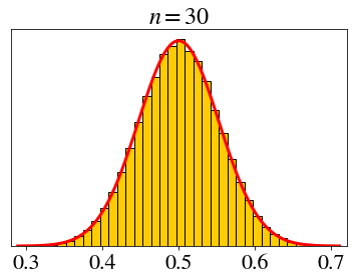
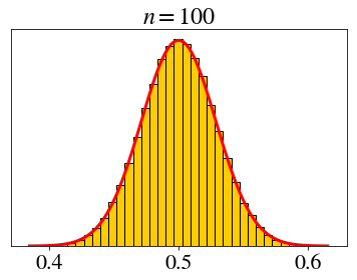
X_i \sim \text{unif}(0, 1),\;\; \bar{X}_n=\frac{X_1+X_2+\cdots+X_n}{n}
\]
Let’s set a fixed x-axis scale.
\[
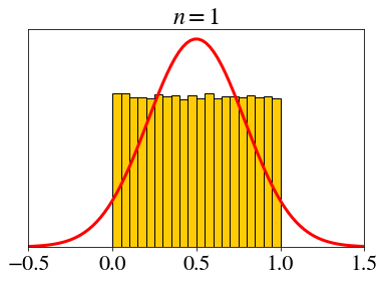
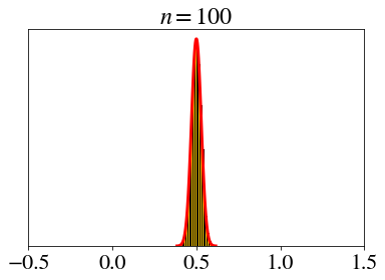
X_i \sim \text{bin}(10, 0.9),\;\; \bar{X}_n=\frac{X_1+X_2+\cdots+X_n}{n}
\]
\[
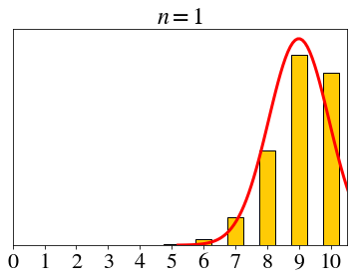
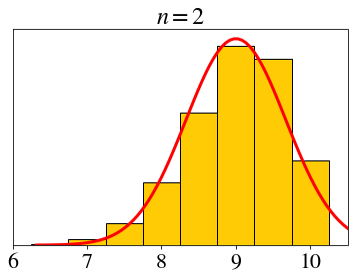
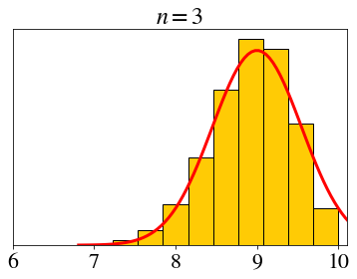
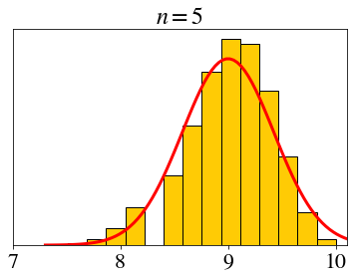
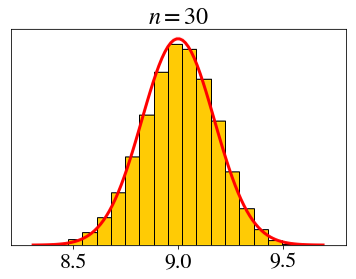
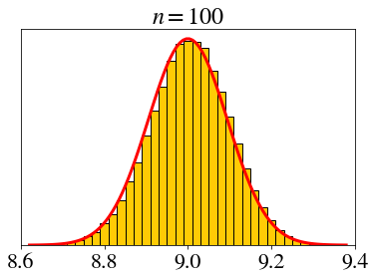
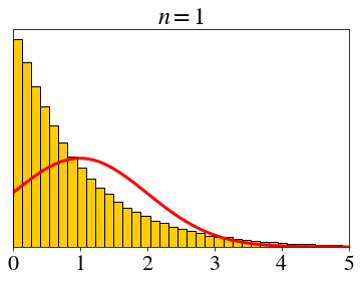
X_i \sim \text{expo}(1),\;\; \bar{X}_n=\frac{X_1+X_2+\cdots+X_n}{n}
\]
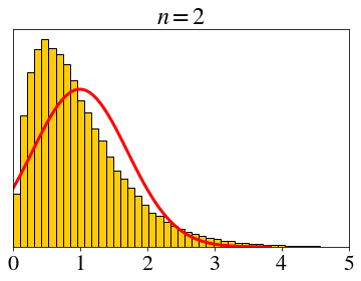
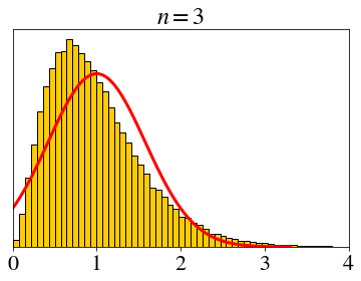
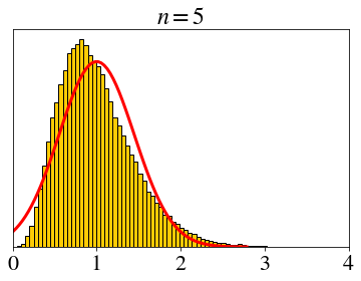
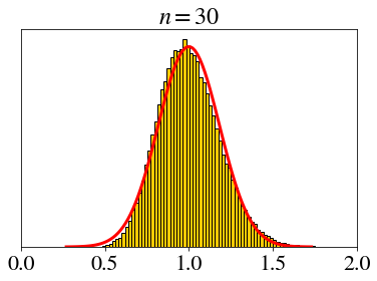
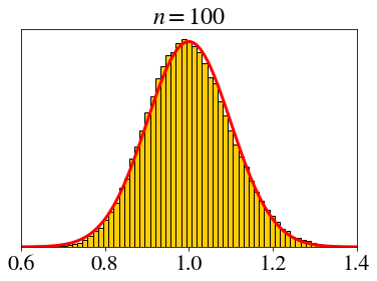
How big does \(n\) need to be for the CLT?
- Not very big.
- Rule of thumb: \(n > 30\)
\[
\text{bin}(10, 0.9)
\]
Exercise
- An accountant rounds each transaction to the nearest dollar (e.g., from $8.63 to $9).
- Assume the error in rounding is \(\text{unif}(-0.5, 0.5)\).
- There is a total of 300 transaction entries today.
- What is the probability that the total error in today’s transactions is more than $5?
