Assume \(X_1, X_2, \cdots, X_n\) are i.i.d. (independent and identically distributed) RVs with mean \(\mu\) and variance \(\sigma^2\).
\[
\bar{X}_n \stackrel{\text{def}}{=} \frac{X_1+X_2+\cdots+X_n}{n}=\frac{1}{n}\sum_{i=1}^n X_i
\]
Loosely speaking, the LLN states that with high probability, the sample mean \((\bar{X}_n)\) of many i.i.d. random variables is very close to the true mean \((\mu)\).
Note \(\bar{X}\) is not a number, but a random variable.
\[
\small{
\begin{aligned}
\bar{X}_n&=\frac{X_1+X_2+\cdots+X_n}{n} \\
\\
\text{E}[\bar{X}_n]&=\frac{\text{E}[X_1]+\text{E}[X_2]+\cdots+\text{E}[X_n]}{n}=\frac{n\mu}{n}=\mu \\
\\
\text{var}(\bar{X}_n)&=\frac{\text{var}(X_1)+\text{var}(X_2)+\cdots+\text{var}(X_n)}{n^2}=\frac{n\sigma^2}{n^2}=\frac{\sigma^2}{n} \\
\end{aligned}
}
\]
We apply the Chebyshev inequality and obtain
\[
\text{P}\big(|\bar{X}_n - \mu| \geq \epsilon \big) \leq \frac{\sigma^2}{n\epsilon^2}, \;\; \text{for all $\epsilon > 0$.}
\]
\[
\text{P}\big(|\bar{X}_n - \mu| \geq \epsilon \big) \leq \frac{\sigma^2}{n\epsilon^2}, \;\; \text{for all $\epsilon > 0$.}
\]
For any fixed \(\epsilon\), the right-hand side of the inequality approaches to zero as \(n\) increases.
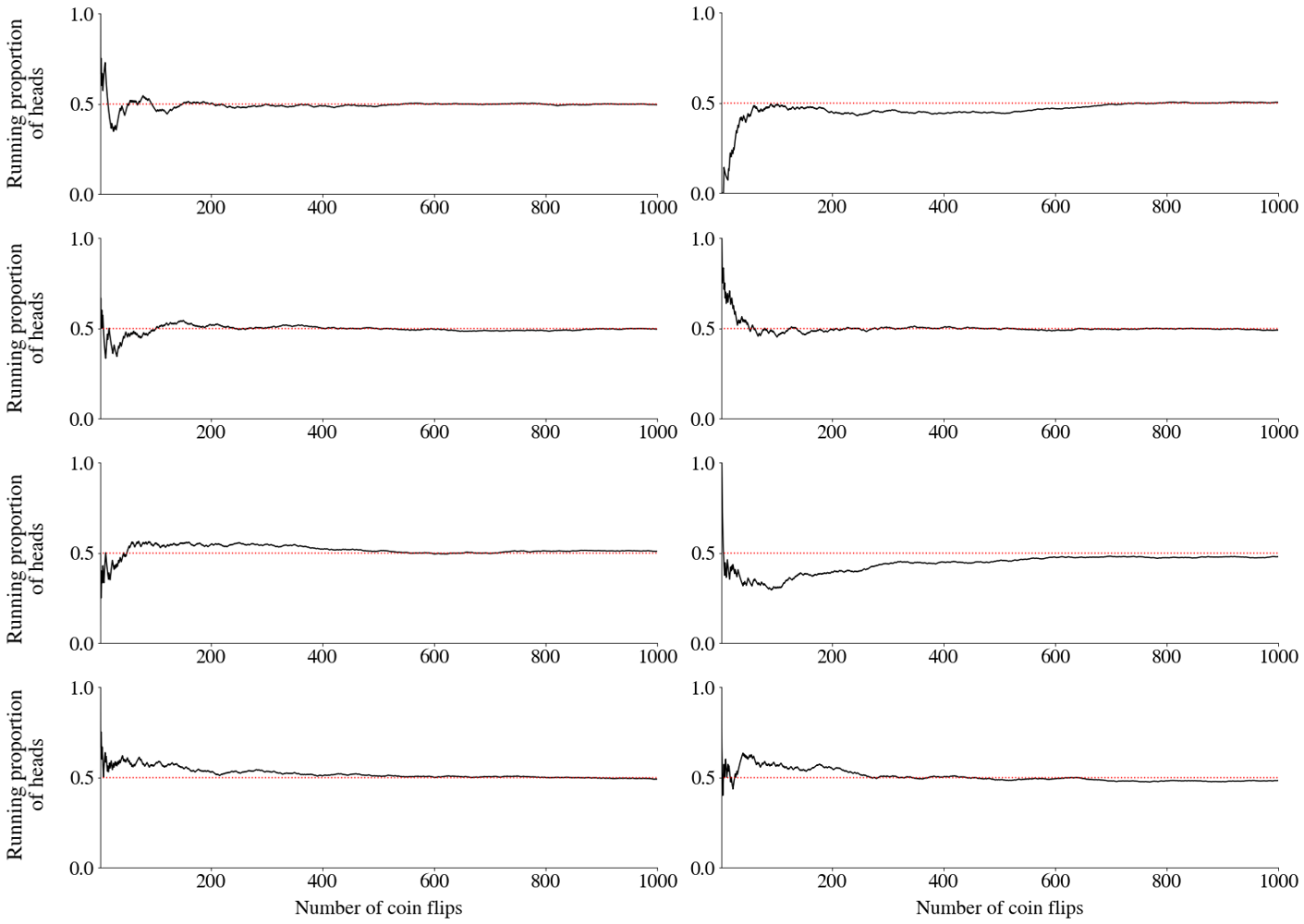
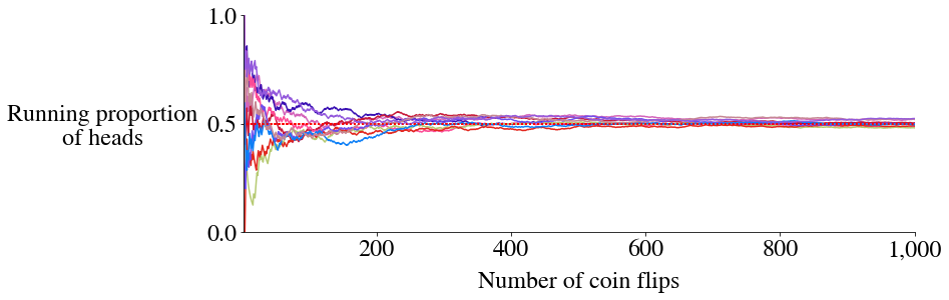
Keep flipping a fair coin many times
Mark a blue dot for heads, a red dot for tails
![]()
Keep flipping a fair coin many times
![]()
Let \(X_1, X_2, \cdots, X_n\) be i.i.d. Bernoulli RV with \(p=0.5\).
\[
\mu = \text{E}[X_i] = 0.5, \;\;\;\;\;\;\bar{X}_n = \frac{1}{n}\sum_{i=1}^n X_i
\]
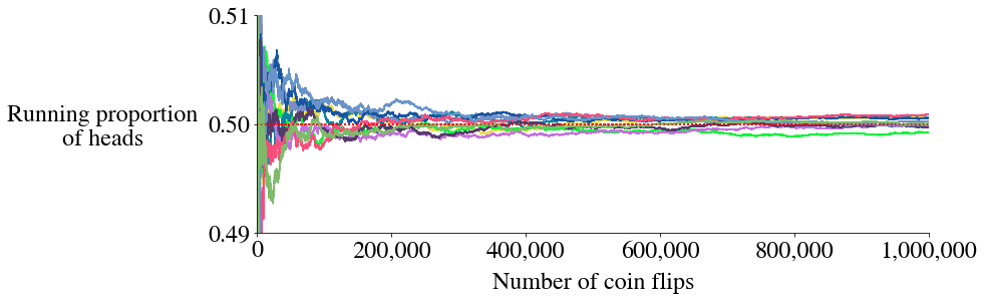
The proportion of heads (\(\bar{X}_n\)) gets closer to 0.5 as \(n\) increases.
The (weak) Law of Large Numbers
Let \(X_1, X_2, \cdots, X_n\) be i.i.d. RVs with mean \(\mu\).
\[
\lim_{n\rightarrow +\infty}\text{P}\big(|\bar{X}_n - \mu| < \epsilon\big)=1, \;\; \text{for every $\epsilon >0$}.
\]
We say the sequence \(\bar{X}_n\) converges to \(\mu\) in probability.
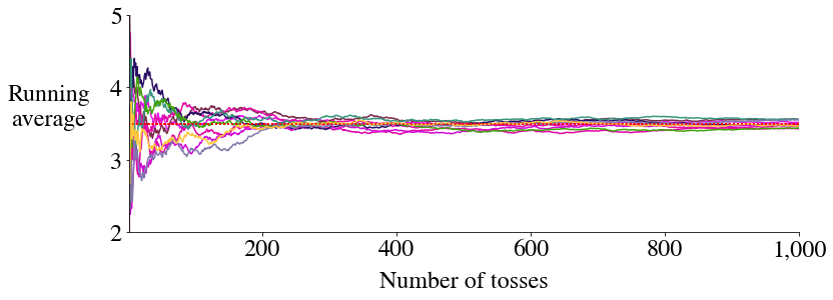
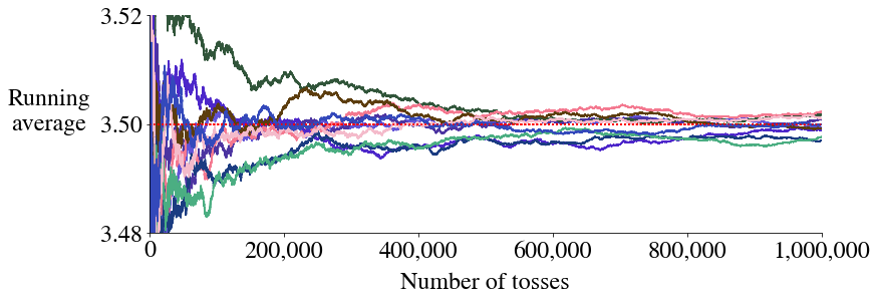
With 8 sequences (simulated data)
![]()
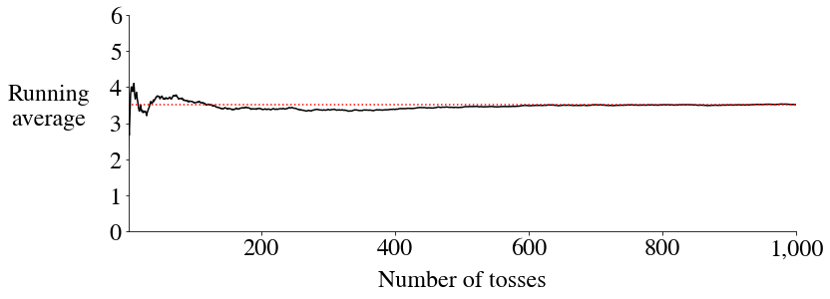
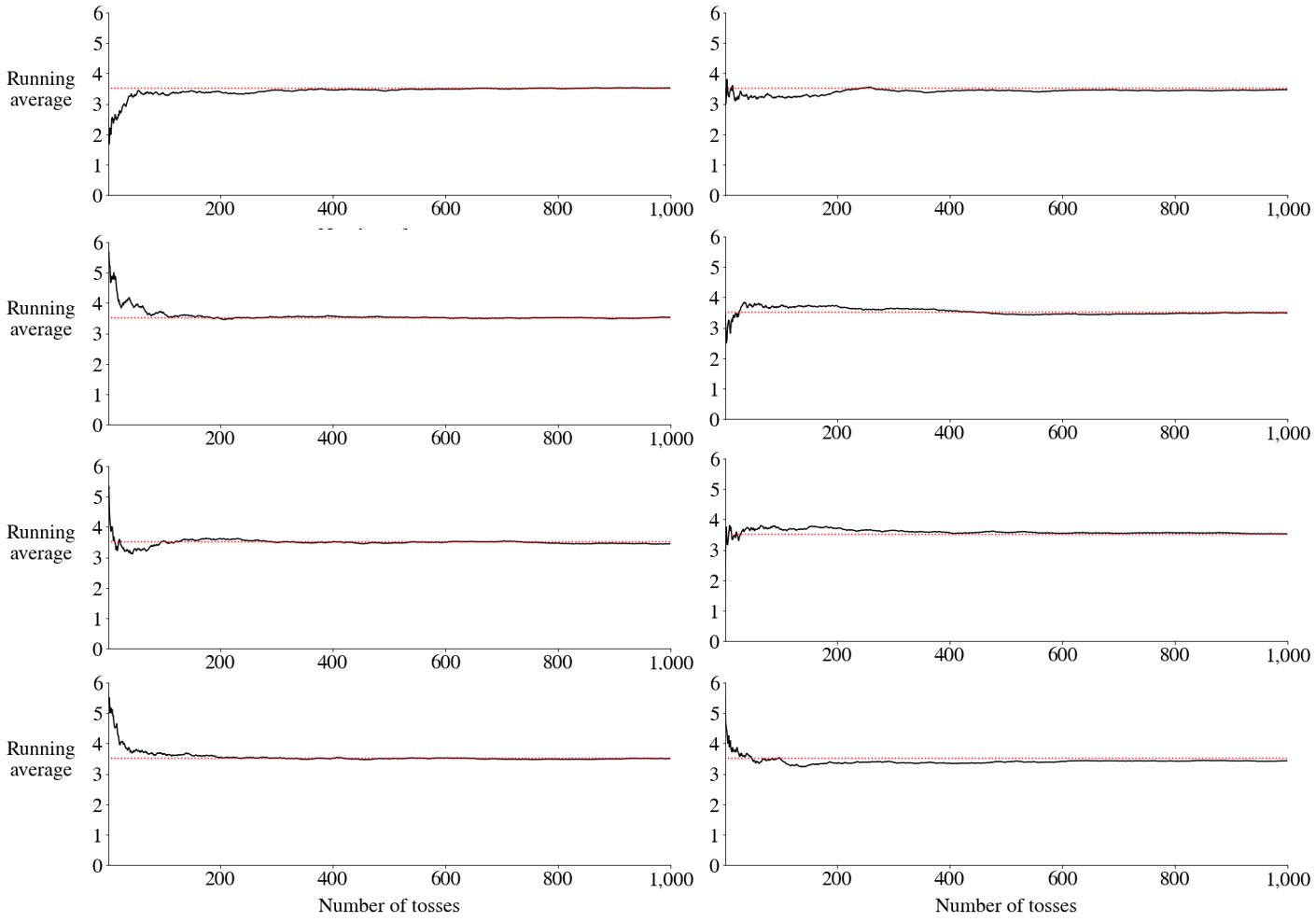
Keep tossing a six-sided die.
![]()
With 8 sequences (simulated data)
![]()
- 37 numbers including 18 reds, 18 blacks, and 1 green.
- Batting red or black with 1:1 payout
- If wheel lands on green, both red and black lose.
- What is a player’s expected net gain for betting $1?
Why casinos don’t lose money
- What are the expected gain for betting other things?
- Odd (1, 3,…, 35) or even (2, 4,…, 36) with 1:1 payout
- Small (1-18) or large(19-36) with 1:1 payout
- Green (0) with 36:1 payout
The best 3-point shooter in NBA
![]()
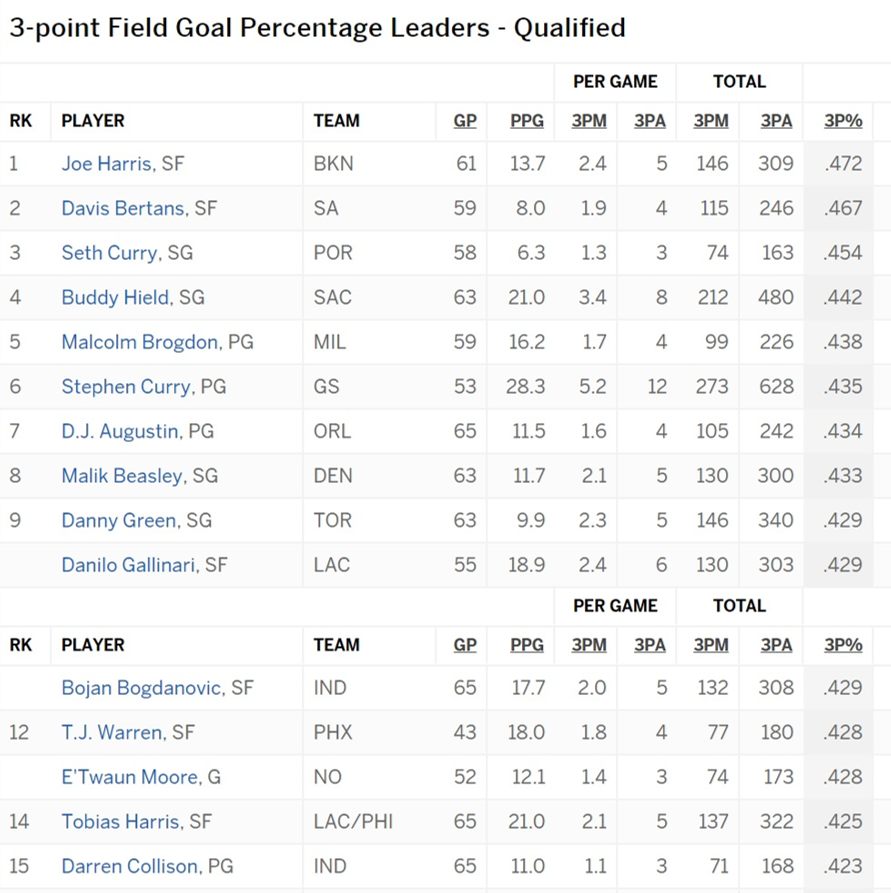
The best 3-point shooter in NBA
![]()
- Does the LLN contradict with the Gambler’s fallacy?
- The law works not by balancing out what has happened.
- It works by diluting what has happened with new data, so that the past is less and less important.
