5.9 Correlation
Correlation coefficient
The correlation coefficient (or simply, correlation) between two RVs \(X\) and \(Y\):
\[ \rho(X, Y) \stackrel{\text{def}}{=} \frac{\text{cov}(X, Y)}{\sqrt{\text{var}(X)\text{var}(Y)}} \]
We can rewrite it as
\[ \rho(X, Y) \stackrel{\text{def}}{=} \text{cov}\bigg(\frac{X-\text{E}[X]}{\sqrt{\text{var}(X)}}, \frac{Y-\text{E}[Y]}{\sqrt{\text{var}(Y)}} \bigg) \]
The correlation is the covariance after standardization.
Properties
\[ \rho(X, Y) \stackrel{\text{def}}{=} \text{cov}\bigg(\frac{X-\text{E}[X]}{\sqrt{\text{var}(X)}}, \frac{Y-\text{E}[Y]}{\sqrt{\text{var}(Y)}} \bigg) \]
\(\rho\) is dimensionless.
For any constants \(a\) and \(b\)
\[ \begin{aligned} \text{cov}(aX+b, Y)&=a\cdot\text{cov}(X, Y) \\ \\ \rho(aX+b, Y)&=\rho(X, Y) \\ \end{aligned} \]
Scaling a variable does not change the correlation.
\[ \begin{aligned} \rho(aX+b, Y)&= \frac{\text{cov}(aX+b, Y)}{\sqrt{\text{var}(aX+b)\text{var}(Y)}} \\ \\ &= \frac{a\cdot\text{cov}(X, Y)}{\sqrt{a^2\text{var}(X)\text{var}(Y)}} \\ \\ &= \frac{\text{cov}(X, Y)}{\sqrt{\text{var}(X)\text{var}(Y)}} \\ \\ &=\rho(X, Y) \\ \end{aligned} \]
Assume we found the correlation between air temperature (in Fahrenheit) and humidity is 0.4.
\[ \rho(\text{Fahrenheit, Humidity}) = 0.4 \]
What is the correlation if the temperature is in Celsius?
\[ \text{Celsius} = \frac{5}{9} (\text{Fahrenheit} - 32) \]
\[ \rho(\text{Celsius, Humidity}) = ? \]
Correlation bounds
For any two RVs \(X\) and \(Y\), we have
\[ -1 \leq \rho(X, Y) \leq 1 \]
\[ \begin{aligned} \rho=1, & \;\text{iff (if and only if) $Y=aX+b$ with $a>0$.} \\ \\ \rho=-1, & \;\text{iff $Y=aX+b$ with $a < 0$.} \\ \end{aligned} \]
\[ \small{ \begin{aligned} &\;\text{var}\bigg(\frac{X}{\sqrt{\text{var}(X)}}+\frac{Y}{\sqrt{\text{var}(Y)}}\bigg) \\ \\ =&\;\text{var}\bigg(\frac{X}{\sqrt{\text{var}(X)}}\bigg)+\text{var}\bigg(\frac{Y}{\sqrt{\text{var}(Y)}}\bigg) \\ &+2\text{cov}\bigg(\frac{X}{\sqrt{\text{var}(X)}}, \frac{Y}{\sqrt{\text{var}(Y)}}\bigg) \\ \\ =&\;1+1+2\rho \\ \\ \geq&\; 0 \end{aligned} } \]
So
\[ \rho \geq -1 \]
Similarly,
\[ \small{ \begin{aligned} &\;\text{var}\bigg(\frac{X}{\sqrt{\text{var}(X)}}-\frac{Y}{\sqrt{\text{var}(Y)}}\bigg) \\ \\ =&\;\text{var}\bigg(\frac{X}{\sqrt{\text{var}(X)}}\bigg)+\text{var}\bigg(\frac{Y}{\sqrt{\text{var}(Y)}}\bigg) \\ &-2\text{cov}\bigg(\frac{X}{\sqrt{\text{var}(X)}}, \frac{Y}{\sqrt{\text{var}(Y)}}\bigg)\\ \\ =&\;1+1-2\rho \\ \\ \geq&\; 0 \end{aligned} } \]
So
\[ \rho \leq 1 \]
Lastly,
\[ \begin{aligned} \rho(X, aX+b)&= \frac{\text{cov}(X, aX+b)}{\sqrt{\text{var}(X)\text{var}(aX+b)}} \\ \\ &= \frac{a\cdot\text{cov}(X, X)}{\sqrt{a^2\text{var}(X)\text{var}(X)}} \\ \\ &= \frac{a}{|a|} \\ \end{aligned} \]
Population covariance & correlation
\[ \begin{aligned} \text{cov}(X, Y)&=\text{E}\big[\big(X-\text{E}[X]\big)\big(Y-\text{E}[Y]\big)\big] \\ \rho&=\frac{\text{cov}(X, Y)}{\sqrt{\text{var}(X) \text{var}(Y)}} \\ \end{aligned} \]
Sample covariance & correlation
\[ \begin{aligned} \text{cov}(x, y)&=\frac{\sum(x_i-\bar{x})(y_i-\bar{y})}{n-1} \\ r&=\frac{\sum(x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum(x_i-\bar{x})^2\sum(y_i-\bar{y})^2}} \\ \end{aligned} \]
\[ \large{r=\frac{\sum(x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum(x_i-\bar{x})^2\sum(y_i-\bar{y})^2}}} \]
\(r\) measures the linear relationship between \(x\) and \(y\).
Calculate correlation with Python
Go to Google Colab and sign in. Open a new notebook.
import numpy as np
import pandas as pd
import seaborn as sns
url = "https://imse317.github.io/data/advertising.csv"
df = pd.read_csv(url)
df.head()# manually calculating correlation coefficient r
x = df["TV"]
y = df["sales"]
Sxy = sum((x - x.mean()) * (y - y.mean()))
Sxx = sum((x - x.mean())**2) # **2 is to square
Syy = sum((y - y.mean())**2)
r = Sxy / np.sqrt(Sxx * Syy) # correlation formula
print(r)- \(x\): ice cream sales
- \(y\): number of people drowning in swimming pool
- Are \(x\) and \(y\) correlated?
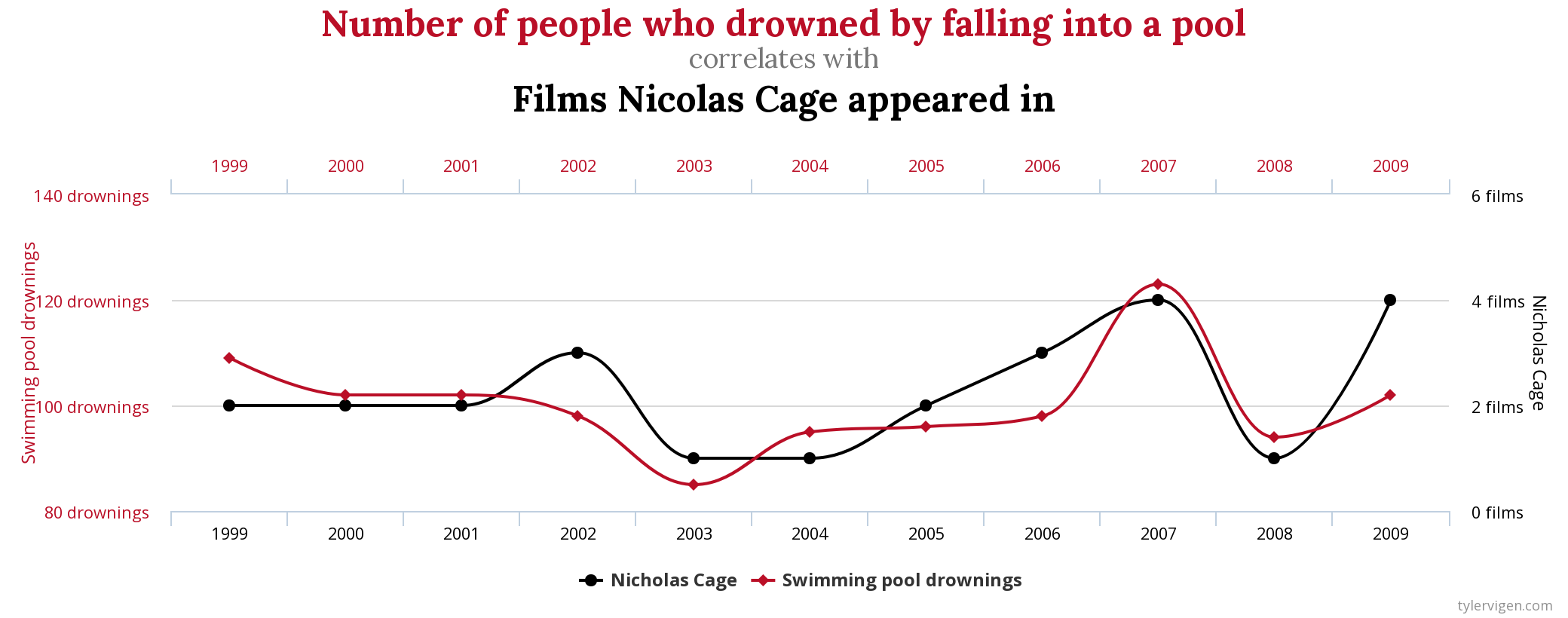
Correlation does not imply causation.
https://xkcd.com/552
Spurious correlations
https://www.tylervigen.com/spurious-correlations