5.5 Conditional PDF
Conditioning
In the discrete case, the conditional PMF of \(X\) given \(Y=y\) is defined by
\[ p_{X \mid Y}(x \mid y)=\frac{p_{X, Y}(x, y)}{p_Y(y)}, \;\; \text{if } p_Y(y)>0. \]
In the continuous case, the conditional PDF of \(X\) given \(Y=y\) is defined by
\[ f_{X \mid Y}(x \mid y)=\frac{f_{X, Y}(x, y)}{f_Y(y)}, \;\; \text{if } f_Y(y)>0. \]
\[ p_{X \mid Y}(x \mid y)=\frac{p_{X, Y}(x, y)}{p_Y(y)} \]
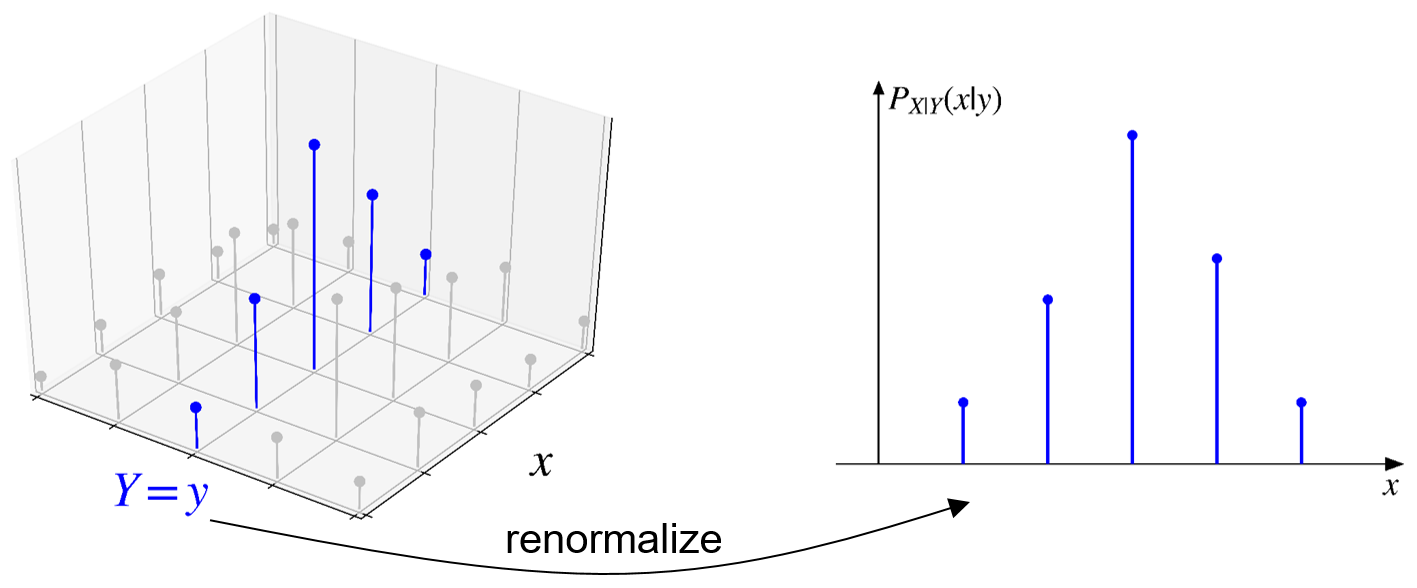
\(p_{X \mid Y}(x \mid y)\) has the same shape as \(p_{X, Y}(x, y)\) at \(Y=y\) except that it is divided by \(p_Y(y)\), which enforce the normalization property.
\[ f_{X \mid Y}(x \mid y)=\frac{f_{X, Y}(x, y)}{f_Y(y)} \]

\(f_{X \mid Y}(x \mid y)\) has the same shape as \(f_{X, Y}(x, y)\) at \(Y=y\) except that it is divided by \(f_Y(y)\), which enforce the normalization property.
Proof \[ \begin{aligned} \int_{-\infty}^{+\infty} f_{X \mid Y}(x \mid y)dx&=\int_{-\infty}^{+\infty} \frac{f_{X,Y}(x,y)}{f_Y(y)}dx \\ \\ &=\frac{1}{f_Y(y)} \int_{-\infty}^{+\infty} f_{X,Y}(x,y)dx \\ \\ &=\frac{1}{f_Y(y)} \; f_Y(y) \\ \\ &=1 \\ \end{aligned} \]
The multiplication rule
In the discrete case,
\[ \begin{aligned} p_{X, Y}(x, y) &= p_X(x) \cdot p_{Y \mid X}(y \mid x) \\ &= p_Y(y) \cdot p_{X \mid Y}(x \mid y) \\ \end{aligned} \]
We can use this formula to calculate the joint PMF.
In the continuous case,
\[ \begin{aligned} f_{X, Y}(x, y)&= f_Y(y) \cdot f_{X \mid Y}(x \mid y) \\ &= f_X(x) \cdot f_{Y \mid X}(y \mid x) \\ \end{aligned} \]
We can use this formula to calculate the joint PDF.
How are the joint, marginal, and conditional PDFs related to each other?
To calculate the joint PDF,
\[ f_{X, Y}(x, y)= f_Y(y) \cdot f_{X \mid Y}(x \mid y) \]
To calculate the marginal PDF
\[ \begin{aligned} f_X(x)&=\int_{-\infty}^{+\infty} f_{X, Y}(x, y)dy \\ &=\int_{-\infty}^{+\infty} f_Y(y) \cdot f_{X \mid Y}(x \mid y)dy \\ \end{aligned} \]
Exercise

- A stick of length \(l\) is broken at a uniformly random point \(X\) on the interval \([0, l]\).
- Given that \(X=x\), another breaking point \(Y\) was chosen uniformly on the interval \([0, x]\).
- What is the PDF of \(Y\)?
\[ X \sim \text{unif}(0, l), \;\; f_{X}(x) = \begin{cases} 1/l, & \text{if $0 \leq x \leq l$,} \\ 0, & \text{otherwise.} \end{cases} \]
\[ \text{Given $X=x$, }\; f_{Y \mid X}(y \mid x) = \begin{cases} 1/x, & \text{if $0 \leq y \leq x$,} \\ 0, & \text{otherwise.} \end{cases} \]
By applying the multiplication rule, we have \[ \begin{aligned} f_{X, Y}(x, y) &= f_{X}(x) \cdot f_{Y \mid X}(y \mid x) \\ \\ &= \begin{cases} 1/(lx), & \text{if $0 \leq y \leq x \leq l$,} \\ 0, & \text{otherwise.} \end{cases} \end{aligned} \]
What is the marginal PDF of \(Y\)?
\[ \begin{aligned} f_{Y}(y) &= \int_{-\infty}^{+\infty} f_{X, Y}(x, y)dx \\ &= \int_y^l \frac{1}{lx}dx \\ &= \frac{1}{l} \ln x \bigg|_y^l \\ &= \frac{1}{l} (\ln l-\ln y) = \frac{1}{l}\ln(\frac{l}{y}) \end{aligned} \]