5.4 Joint & marginal PDF

Probability density function (PDF)

Recall that a RV \(X\) is called continuous if there is a nonnegative function \(f_X\), such that

\[ \begin{aligned} &\text{P}(X \in B)=\int_B f_X dx \\ \\ &\text{for every subset $B$ of the real line.} \\ \end{aligned} \]

Consider two continuous RVs \(X\) and \(Y\) from the same experiment.

The joint PDF is a nonnegative function that satisfies

\[ \text{P}\big((X, Y) \in A\big)=\iint\limits_{(x, y) \in A} f_{X, Y}(x, y) dxdy \]

The integration is carried over \(A\) on the 2-D plane.

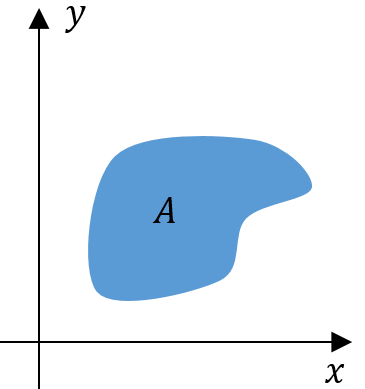
\[ \text{P}\big((X, Y) \in A\big)=\iint\limits_{(x, y) \in A} f_{X, Y}(x, y) dxdy \]

\[ \text{Let } A=\{(x, y) \mid a < x < b, c < y < d\} \]

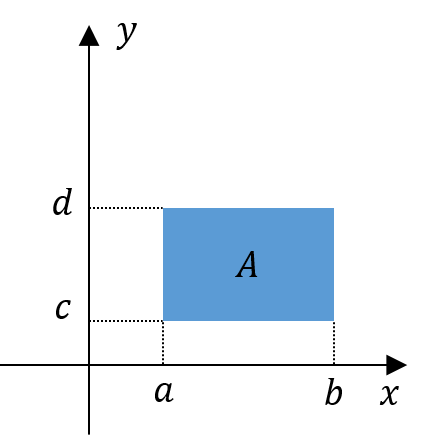
\[ \text{P}(a < x < b, \; c < y < d)=\int_c^d \int_a^b f_{X, Y}(x, y)dxdy \]

Single continuous RV

\[ \text{P}(a < X < b)=\int_a^b f_X dx \]

The probability is the area under the density curve.

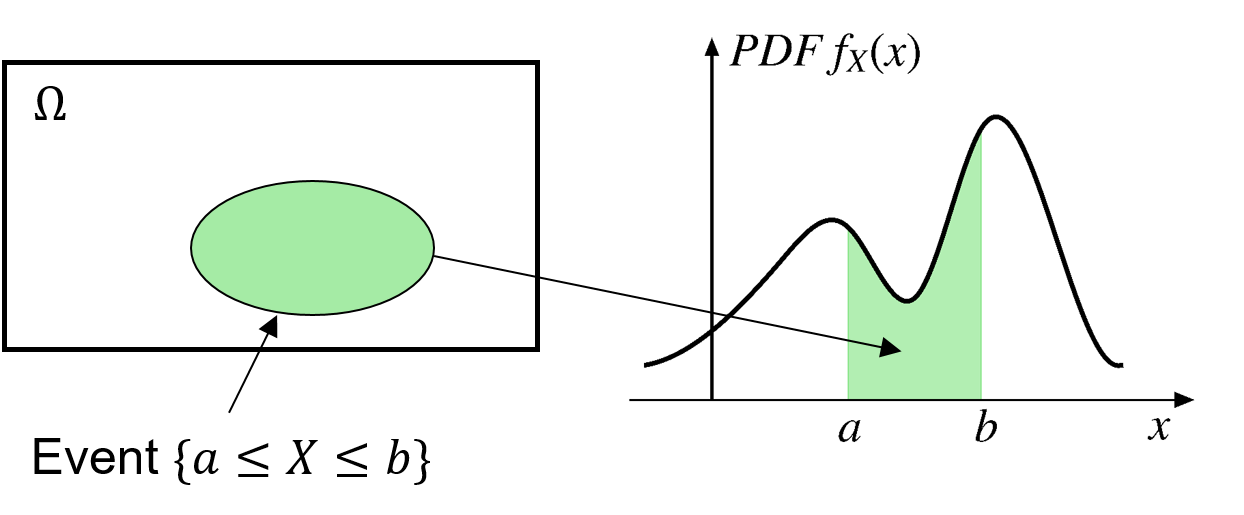
Two continuous RVs

\[ \text{P}(a < x < b, \; c < y < d)=\int_c^d \int_a^b f_{X, Y}(x, y)dxdy \]

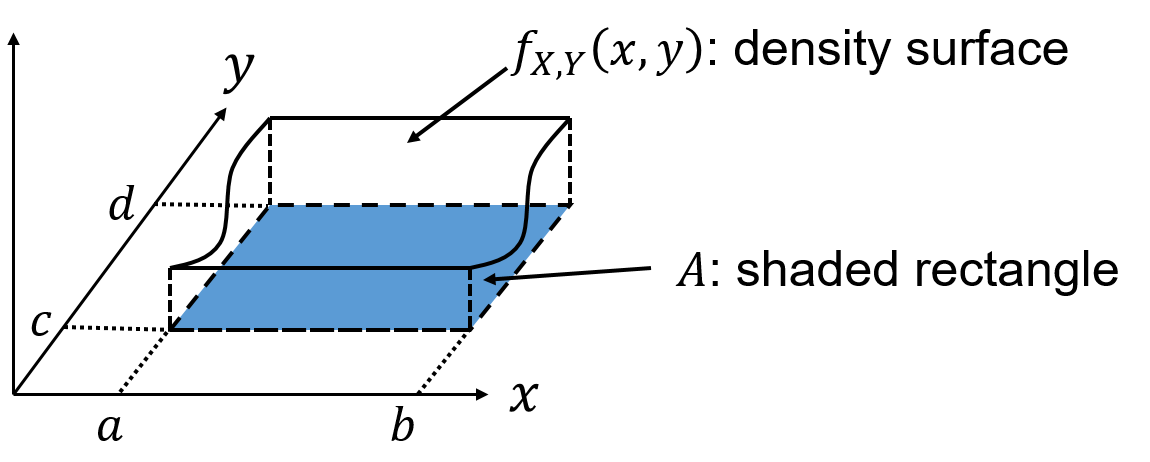
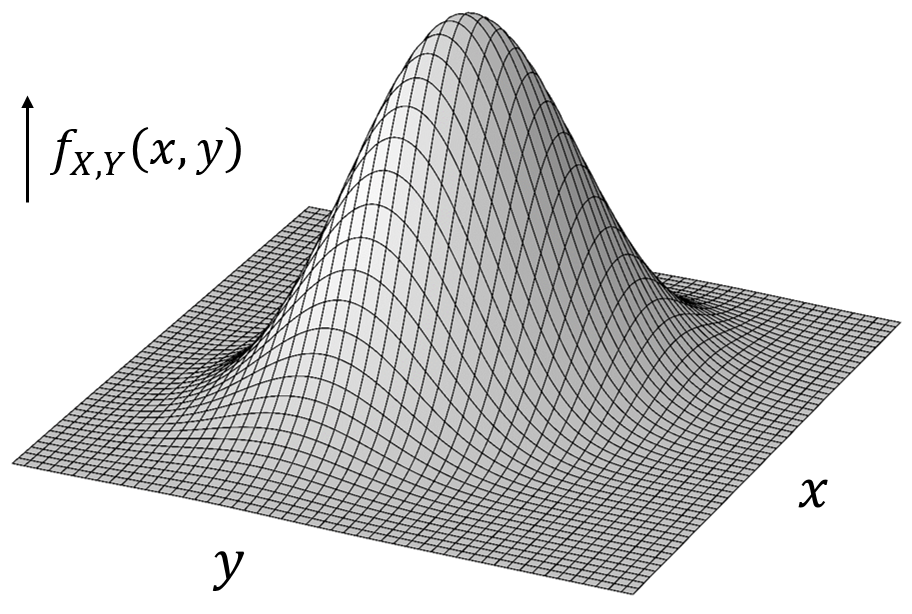
The probability is the volume under the density surface.

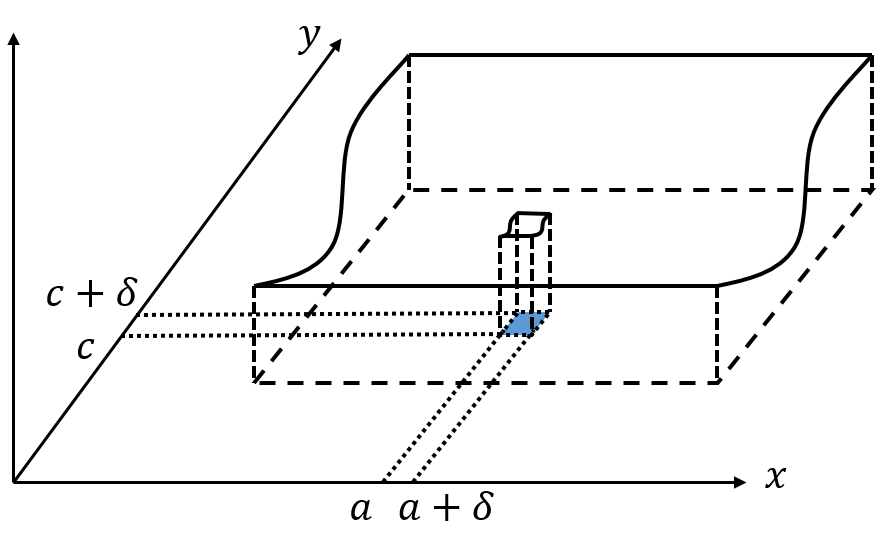
\[ \begin{aligned} &\text{P}(a < x < a+\delta, c < y < c+\delta) \\ \\ =\;&\int_c^{c+\delta} \int_a^{a+\delta} f_{X, Y}(x, y)dxdy \\ \\ \approx \;& f_{X, Y}(a, c) \cdot \delta ^2 \\ \end{aligned} \]

\(f_{X, Y}(a, c)\) is the probability per unit area in the vicinity of \((a, c)\).

Visualization of joint PDF

The normalization property (1-D)

For a single continuous RV, we have \(\int_{-\infty}^{+\infty} f_X dx=1\).

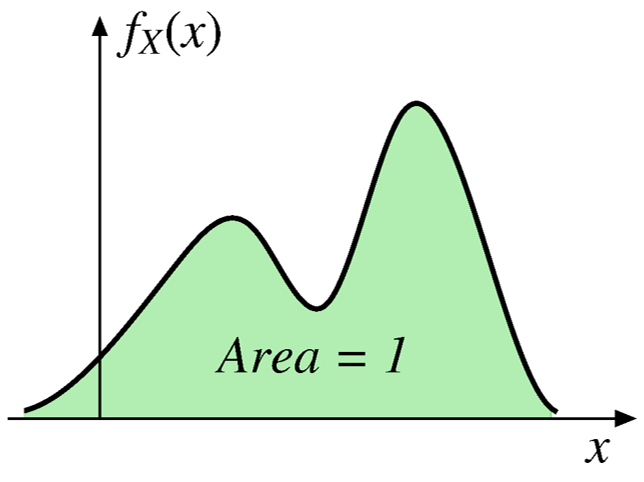
The total area under the density curve is 1.

The normalization property (2-D)

For two continuous RVs \(X\) and \(Y\), we have

\[ \small{ \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f_{X, Y}(x, y) dxdy=1 } \]

The total volume under the density surface is 1.

Marginal PDF

For discrete RVs \(\color{red}{X}\) and \(\color{blue}{Y}\), the marginal PMFs are \[ p_\color{red}{X}(\color{red}{x})=\sum_\color{blue}{y} p_{X, Y}(x, y) \]

\[ p_\color{blue}{Y}(\color{blue}{y})=\sum_\color{red}{x} p_{X, Y}(x, y) \]

For continuous RVs \(\color{red}{X}\) and \(\color{blue}{Y}\), the marginal PDFs are \[ f_\color{red}{X}(\color{red}{x})=\int_{-\infty}^{+\infty} f_{X, Y}(x, y) d\color{blue}{y} \]

\[ f_\color{blue}{Y}(\color{blue}{y})=\int_{-\infty}^{+\infty} f_{X, Y}(x, y) d\color{red}{x} \]

Integrate the joint PDF over all possible values of the other variable.

Let \((X, Y)\) be a random point on the unit square.

What is its joint PDF?

\[ f_{X, Y}(x, y) = \begin{cases} c, & \text{if $x, y \in [0, 1]$,} \\ 0, & \text{otherwise.} \end{cases} \]

To satisfy the normalization property

\[ \small{ \begin{aligned} \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f_{X, Y}(x, y) dxdy &=\int_0^1 \int_0^1 c \; dxdy \\ \\ &=c \int_0^1 \int_0^1 1 \; dxdy \\ \\ &=c \end{aligned} } \]

We must set \(c=1\).

\[ \small{ f_{X, Y}(x, y) = \begin{cases} 1, & \text{if $x, y \in [0, 1]$,} \\ 0, & \text{otherwise.} \end{cases} } \]

What is the marginal PDF of \(X\)?

\[ \small{ \text{If $x < 0$ or $x > 1$,}\; f_X(x)=\int_{-\infty}^{+\infty} f_{X, Y}(x, y) dy =\int_{-\infty}^{+\infty} 0 \; dy=0 } \]

\[ \small{ \text{If $x \in [0, 1]$,}\; f_X(x)=\int_{-\infty}^{+\infty} f_{X, Y}(x, y) dy=\int_0^1 1 \; dy =1 } \]

\[ X \sim \text{unif}(0, 1) \]

\[ f_{X, Y}(x, y) = \begin{cases} 1, & \text{if $x, y \in [0, 1]$,} \\ 0, & \text{otherwise.} \end{cases} \]

\[X \sim \text{unif}(0, 1)\]

What is the marginal PDF of \(Y\)?

\[ Y \sim \text{unif}(0, 1) \]

Uniform joint PDF

More generally, let \(S\) be a subset of the 2-D plane.

The corresponding uniform joint PDF on \(S\) is

\[ \small{ f_{X, Y}(x, y) = \begin{cases} \frac{1}{\text{area of $S$}}, & \text{if $(x, y) \in S$,} \\ 0, & \text{otherwise.} \end{cases} } \]

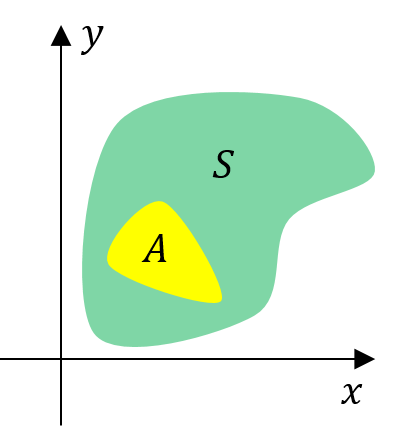
\[ \small{ \begin{aligned} \text{P}\big((X, Y) \in A\big)&=\iint\limits_{(x, y) \in A} f_{X, Y}(x, y) dxdy \\ &=\iint\limits_{(x, y) \in A} \frac{1}{\text{area of $S$}} dxdy \\ &=\frac{1}{\text{area of $S$}}\iint\limits_{(x, y) \in A} 1 \;dxdy \\ &=\frac{\text{area of $A$}}{\text{area of $S$}} \\ \end{aligned} } \]

Uniform dist. on the unit square

\[ f_{X, Y}(x, y) = \begin{cases} 1, & \text{if $x, y \in [0, 1]$,} \\ 0, & \text{otherwise.} \end{cases} \]

What is the probability that \(X < Y\)?

\[ \small{ \begin{aligned} \text{P}(X < Y) &= \frac{\text{area of yellow}}{\text{area of green}}\\ &= \frac{1/2}{1}=0.5 \end{aligned} } \]

Uniform dist. on the unit disk

Let \((X, Y)\) be a random point on the unit disk.

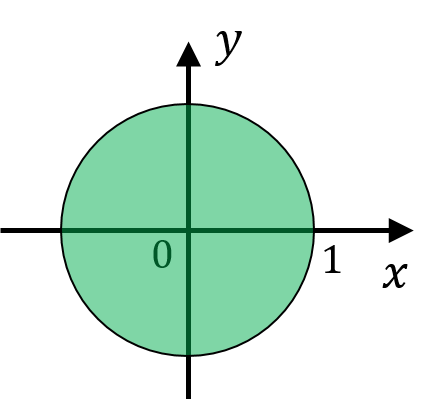
What is its joint PDF?

\[ f_{X, Y}(x, y) = \begin{cases} 1/\pi, & \text{if $x^2+y^2 \leq 1$,} \\ 0, & \text{otherwise.} \\ \end{cases} \]