Conditional PMF
The conditional PMF of \(X\) given \(Y=y\) is defined by
\[
\begin{aligned}
p_{X \mid Y}(x \mid y)&=\text{P}(X=x \mid Y=y) \\
\\
&=\frac{\text{P}(X=x, Y=y)}{\text{P}(Y=y)} \\
\\
&=\frac{p_{X, Y}(x, y)}{p_Y(y)} \\
\end{aligned}
\]
\[
p_{X \mid Y}(x \mid y)=\frac{p_{X, Y}(x, y)}{p_Y(y)}
\]
![]()
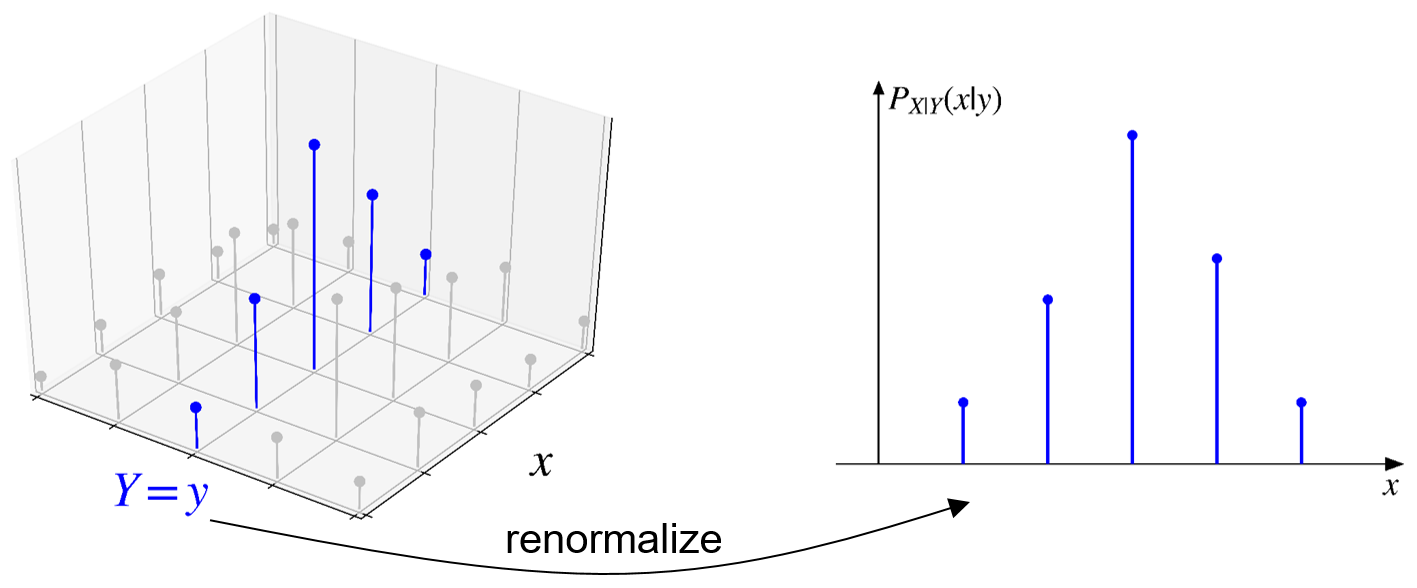
\(p_{X \mid Y}(x \mid y)\) has the same shape as \(p_{X, Y}(x, y)\) at \(Y=y\) except that it is divided by \(p_Y(y)\) to enforce the normalization property.
\[
\begin{aligned}
\sum_x p_{X \mid Y}(x \mid y)&=\sum_x \frac{p_{X,Y}(x,y)}{p_Y(y)} \\
\\
&=\frac{1}{p_Y(y)} \sum_x p_{X,Y}(x,y) \\
\\
&=\frac{1}{p_Y(y)} \; p_Y(y) \\
\\
&=1 \\
\end{aligned}
\]
\(X\): whether they are a current smoker
\(Y\): whether they will develop lung cancer at some point
| \(X=0\) |
\(72\%\) |
\(3\%\) |
\(75\%\) |
| \(X=1\) |
\(20\%\) |
\(5\%\) |
\(25\%\) |
| \(p_Y(y)\) |
\(92\%\) |
\(8\%\) |
\(100\%\) |
If an individual developed lung cancer, what is the probability that they are a current smoker?
\(X\): whether they are a current smoker
\(Y\): whether they will develop lung cancer at some point
| \(X=0\) |
\(72\%\) |
\(3\%\) |
\(75\%\) |
| \(X=1\) |
\(20\%\) |
\(5\%\) |
\(25\%\) |
| \(p_Y(y)\) |
\(92\%\) |
\(8\%\) |
\(100\%\) |
If an individual is a current smoker, what is the probability that they will develop lung cancer?
Slice view of conditional PMF
\[
p_{X \mid Y}(x \mid y)=\frac{p_{X, Y}(x, y)}{p_Y(y)}
\]
![]()
Slice view of conditional PMF
\[
p_{Y \mid X}(y \mid x)=\frac{p_{X, Y}(x, y)}{p_X(x)}
\]
![]()
\[
\begin{aligned}
p_{X \mid Y}(x \mid y)&=\frac{p_{X, Y}(x, y)}{p_Y(y)} \\
p_{X, Y}(x, y) &= p_Y(y) \cdot p_{X \mid Y}(x \mid y) \\
\end{aligned}
\]
Similarly,
\[
\begin{aligned}
p_{Y \mid X}(y \mid x)&=\frac{p_{X, Y}(x, y)}{p_X(x)} \\
p_{X, Y}(x, y) &= p_X(x) \cdot p_{Y \mid X}(y \mid x)\\
\end{aligned}
\]
We often can use this formula to calculate the joint PMF.
\[
\begin{aligned}
p_{X, Y}(x, y) &= p_X(x) \cdot p_{Y \mid X}(y \mid x) \\
\\
&= p_Y(y) \cdot p_{X \mid Y}(x \mid y) \\
\end{aligned}
\]
Does this look like something we have learned before?
This is the counterpart of the multiplication rule.
\[
\begin{aligned}
\text{P}(A \cap B) &= \text{P}(A) \cdot \text{P}(B \mid A) \\
\\
&= \text{P}(B) \cdot \text{P}(A \mid B) \\
\end{aligned}
\]
