5.1 Joint & marginal PMF
- Randomly select a person from a population.
- Record their age and # of credit cards they own.
Two discrete RV \(X\) and \(Y\) from the same experiment.
\((x, y)\) is a pair of possible values of \(X\) and \(Y\).
The joint PMF of \(X\) and \(Y\) is defined as
\[ p_{X, Y}(x, y)=\text{P}\big(\{X=x\} \cap \{Y=y\}\big) \]
For simplicity, we often use the abbreviated notation.
\[ p_{X, Y}(x, y)=\text{P}(X=x, Y=y) \]
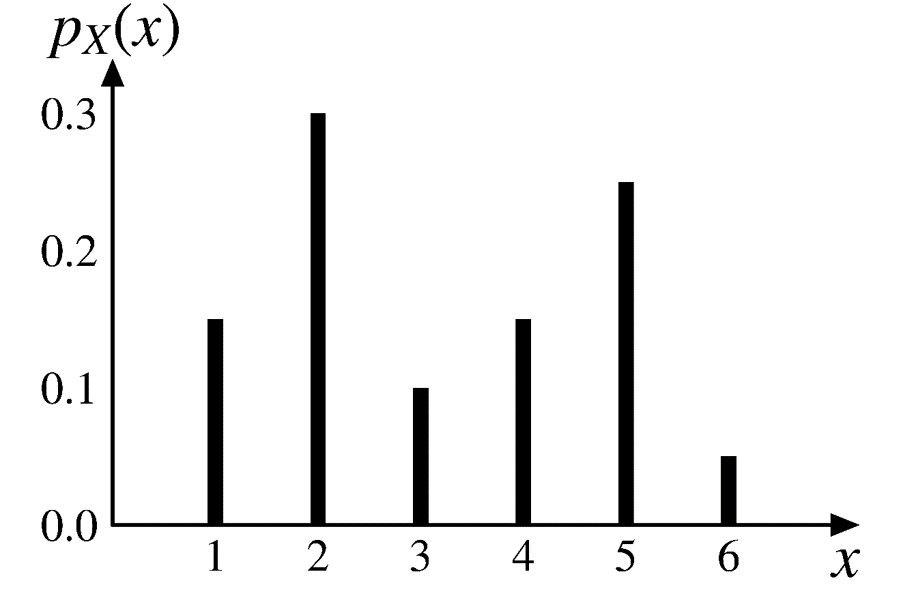
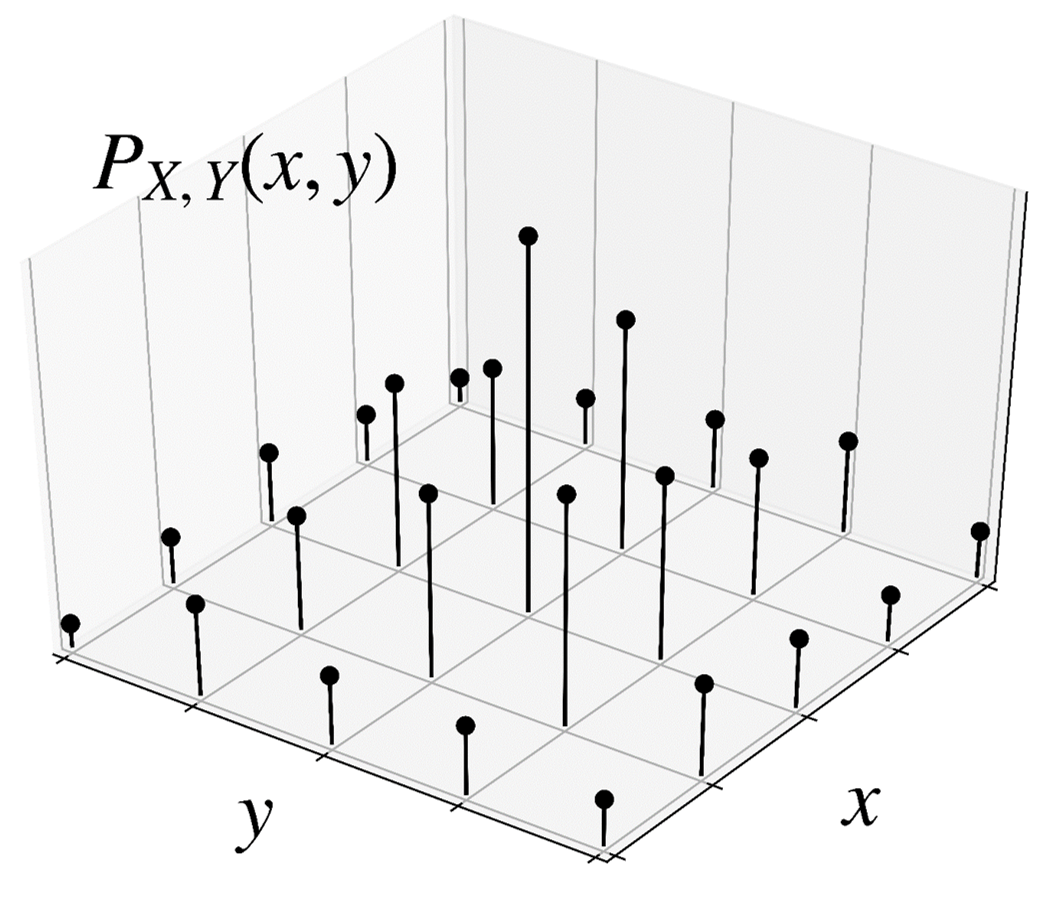
PMF visualization
Joint PMF visualization
We randomly sample an adult from the MI population.
- \(X\): whether they are a current smoker
- \(Y\): whether they will develop lung cancer at some point
Suppose the joint PMF is as follows.
\(Y=0\) \(Y=1\) \(X=0\) \(72\%\) \(3\%\) \(X=1\) \(20\%\) \(5\%\)
Non-negativity
PMF of a single discrete RV \(X\)
\[ p_X(x) \geq 0, \;\; \text{for all $x$.} \]
Joint PMF of two discrete RVs \(X\) and \(Y\)
\[ p_{X, Y}(x, y) \geq 0, \;\;\;\; \text{for all $x$ and $y$.} \]
Normalization property
- For a single discrete RV \(X\), we have \(\sum_x p_X(x)=1\).
- Joint PMF of two discrete RVs \(X\) and \(Y\) \[ \sum_x\sum_y p_{X, Y}(x, y)=1 \]
| \(Y=0\) | \(Y=1\) | |
|---|---|---|
| \(X=0\) | \(72\%\) | \(3\%\) |
| \(X=1\) | \(20\%\) | \(5\%\) |
Cumulative Distribution Function
The CDF of a RV \(X\) is (always) defined by
\[ F_X(x)=\text{P}(X \leq x), \;\; \text{for all $x$.} \]
The joint CDF of two RVs \(X\) and \(Y\) is defined by
\[ F_{X, Y}(x, y)=\text{P}(X \leq x, Y \leq y), \;\;\;\;\;\text{for all $x$ and $y$.} \]
Joint CDFs are generally harder to work with than joint PMFs.
For this reason, we will mainly stick with joint PMFs.
Calculate probabilities from joint PMF
\(A\): the set of all pairs \((x, y)\) that have a certain property.
\[ \text{P}\big((X, Y) \in A\big)=\sum_{(x, y) \in A}p_{X, Y}(x, y) \]
Marginal PMF
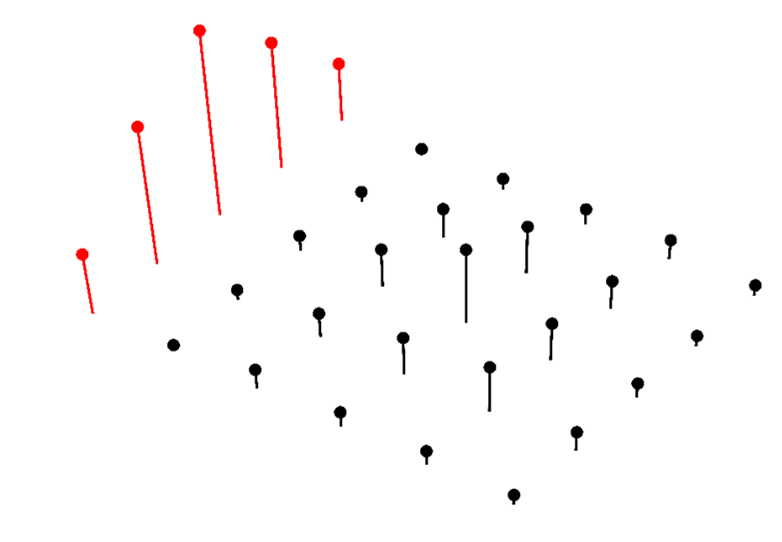
We can calculate the PMF of \(X\) using
\[ \small{ p_X(x)=\text{P}(X=x)=\sum_\color{blue}{y} \text{P}(X=x, Y=y) =\sum_\color{blue}{y} p_{X, Y}(x, y) } \]
We refer to \(p_X(x)\) as the marginal PMF of \(X\).
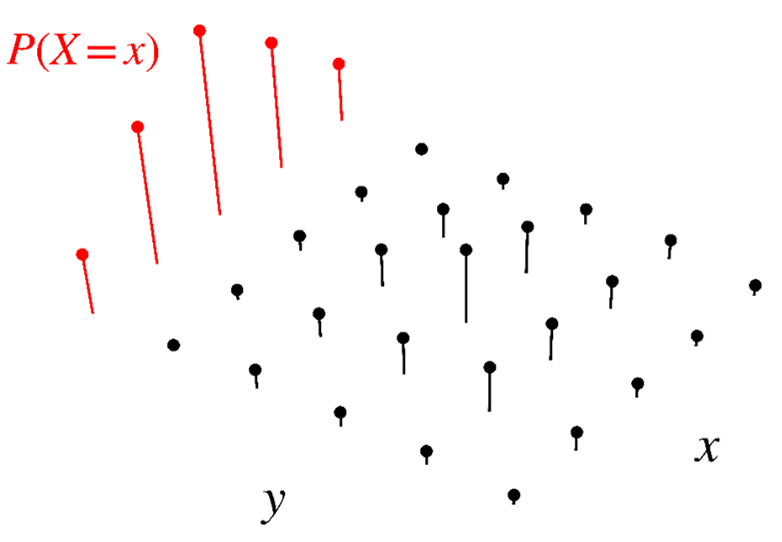
Similarly, we can calculate the PMF of \(Y\) using
\[ \small{ p_Y(y)=\text{P}(Y=y)=\sum_\color{red}{x} \text{P}(X=x, Y=y)=\sum_\color{red}{x} p_{X, Y}(x, y) } \]
We refer to \(p_Y(y)\) as the marginal PMF of \(Y\).
We randomly sample an adult from the MI population.
- \(X\): whether they are a current smoker
- \(Y\): whether they will develop lung cancer at some point
Suppose the joint PMF is as follows.
\(Y=0\) \(Y=1\) \(X=0\) \(72\%\) \(3\%\) \(X=1\) \(20\%\) \(5\%\) What are the marginal PMFs of \(X\) and \(Y\)?