4.4 Continuous uniform distribution
Continuous uniform distribution
- The continuous counterpart of the discrete uniform RV.
- A RV \(X\) that takes values in an interval \([a, b]\).
- Any two sub-intervals of the same length have the same probability.
\[X \sim \text{unif}(a, b)\]
Uniform distribution
Any two values in the interval \([a, b]\) have the same probability density.
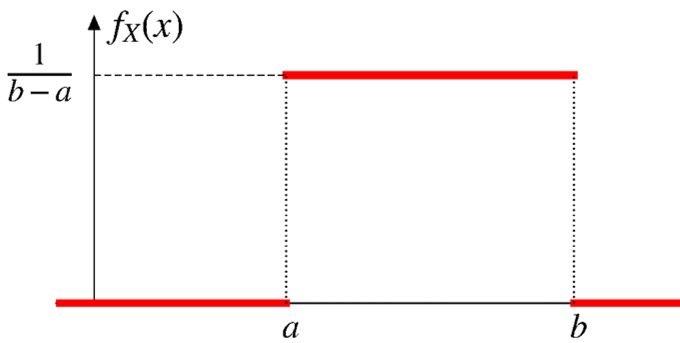
Probability density function
\[ f_X(x) = \begin{cases} \frac{1}{b-a}, & \text{if $a < x < b$}, \\ 0, & \text{otherwise.} \end{cases} \]
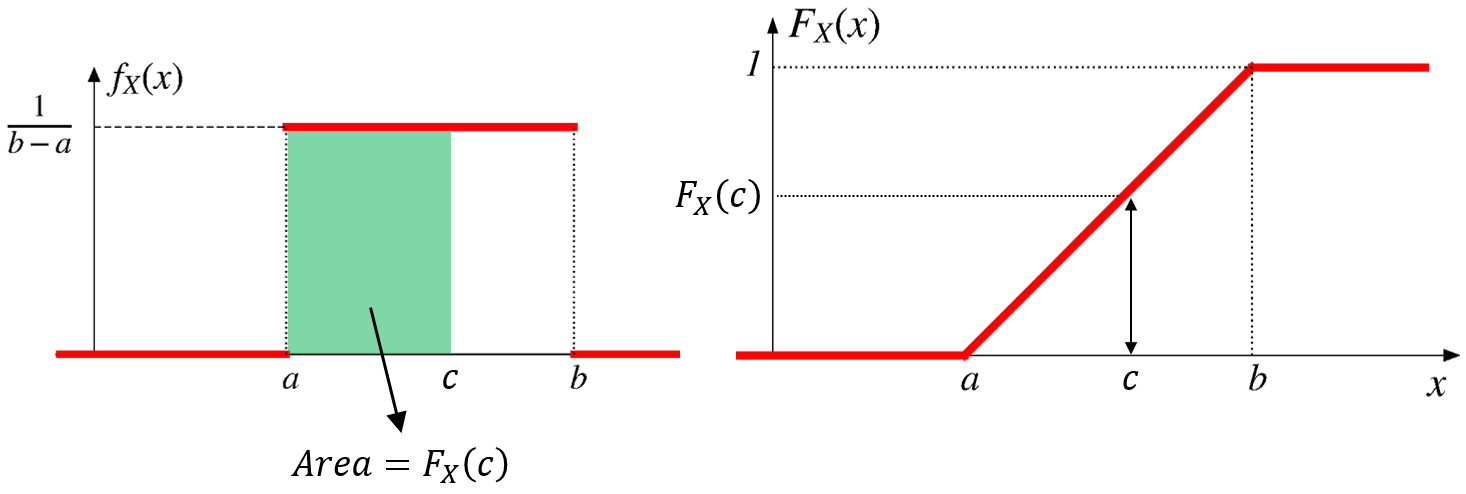
\[ \begin{aligned} F_X(x)&=\int_{-\infty}^x f_X(t) dt \\ \\ &= \begin{cases} 0, & \text{if $x \leq a$,} \\\ \frac{x-a}{b-a}, & \text{if $a < x < b$,} \\ 1, & \text{if $x \geq b$.} \\ \end{cases} \end{aligned} \]
Standard uniform RV
\[ U \sim \text{unif}(0, 1) \]
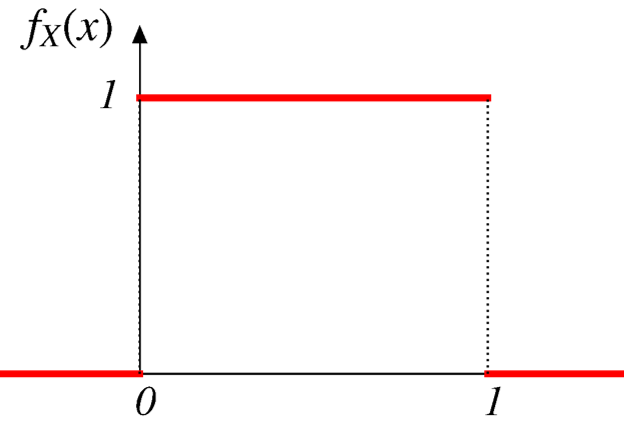
\[ \small{ f_U(u) = \begin{cases} 1, & \text{if $0 < u < 1$,} \\ 0, & \text{otherwise.} \end{cases} } \]
\[ \small{ F_U(u)= \begin{cases} 0, & \text{if $u \leq 0$,} \\ u, & \text{if $0 < u < 1$,} \\ 1, & \text{if $u \geq 1$.} \\ \end{cases} } \]