4.2 Continuous CDF
A cumulative distribution function is always defined as
\[ F_X(x)=\text{P}(X \leq x) \]
\[ \text{If $X$ is discrete,} \;\;\;\; \text{P}(X \leq x)=\sum_{k \leq x}p_X(k) \]
\[ \text{If $X$ is continuous,} \;\;\;\; \text{P}(X \leq x)=\int_{-\infty}^x f_X(t) dt \]
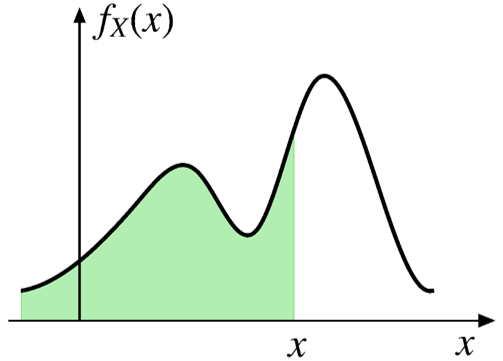
\[ \small{ F_X(x)=\text{P}(X \leq x)=\int_{-\infty}^x f_X(t) dt } \]
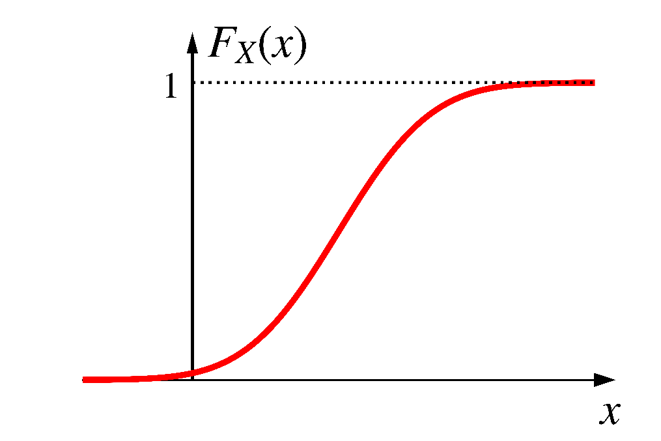
\[ \small{0 < F_X(x) < 1,\;\; \lim_{x\rightarrow-\infty}F_X(x)=0,\;\; \lim_{x \rightarrow +\infty}F_X(x)=1} \]
\[ \small{\text{$F_X$ is non-decreasing.}} \]
Calculate probability using CDF
\[ \text{For any constant $a$,} \]
\[ \text{P}(X>a)=1-F_X(a) \]
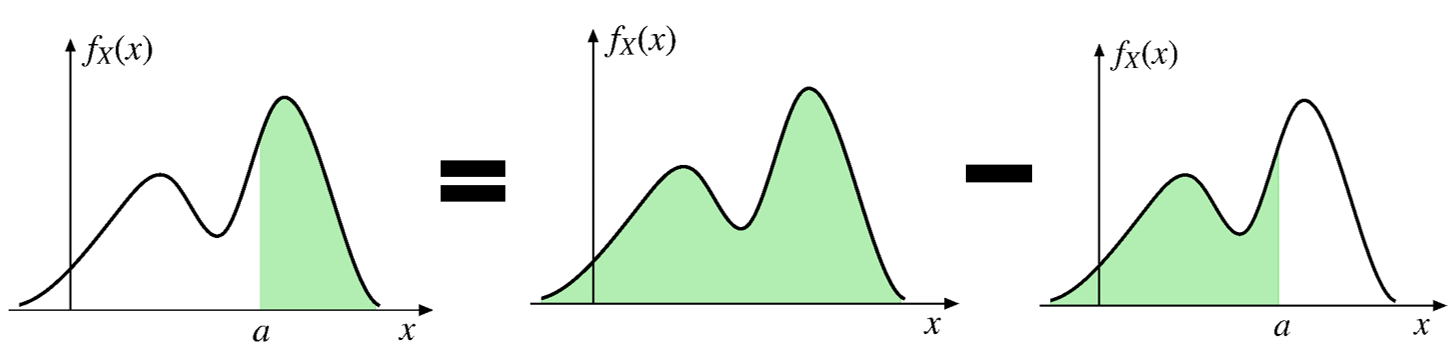
Calculate probability using CDF
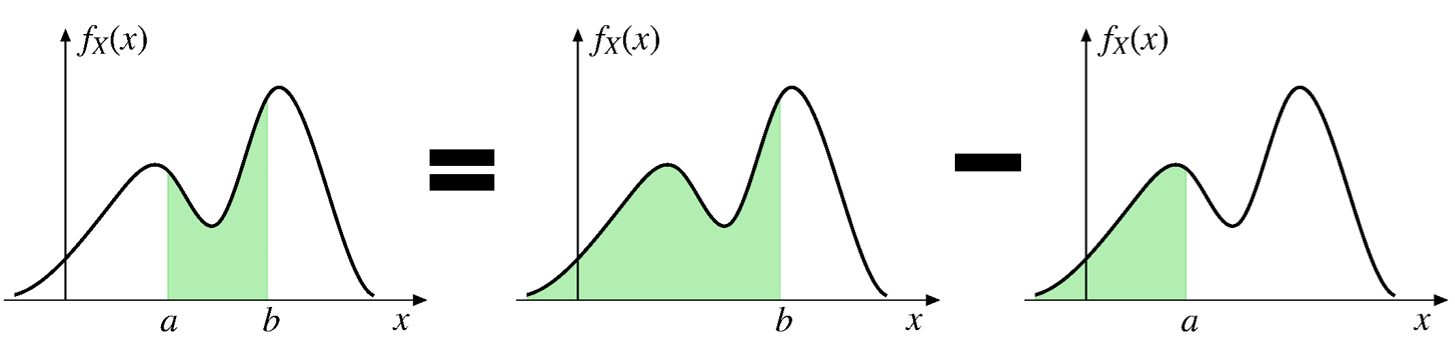
\[ \text{For any two constants $a$ and $b$ with $a < b$,} \]
\[ \text{P}(a < X < b )=F_X(b)-F_X(a) \]
