4.1 Probability density function
Continuous variables
- It can take on infinitely many, uncountable values.
- If it can take on two particular values, it can also take on all the values between them.
- Examples
- Speed of riding a bicycle
- Water level of a dam
- Customer arrival time at a store
Continuous random variables
A RV \(X\) is called continuous if there is a nonnegative function \(f_X\), such that for every subset \(B\) of the real line
we have
\[
\text{P}(X \in B)=\int_B f_X dx
\]
In particular, for one interval \([a, b]\)
\[
\text{P}(a \leq X \leq b)=\int_a^b f_X dx
\]
The probability is the definite integral of \(f_X(x)\) from \(a\) to \(b\).
\[
\text{P}(a \leq X \leq b)=\int_a^b f_X dx
\]
\(f_X\) is called the probability density function (PDF) of \(X\).
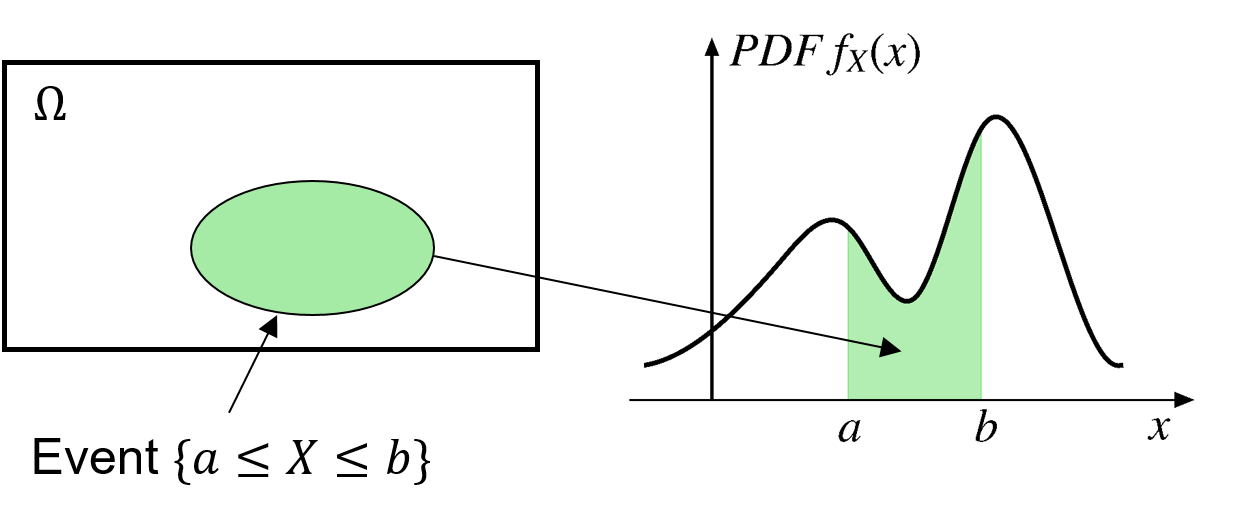
For a discrete RV, \(p_X\) is called the probability mass function.
Why \(f_X\) is called the probability density function?
\[
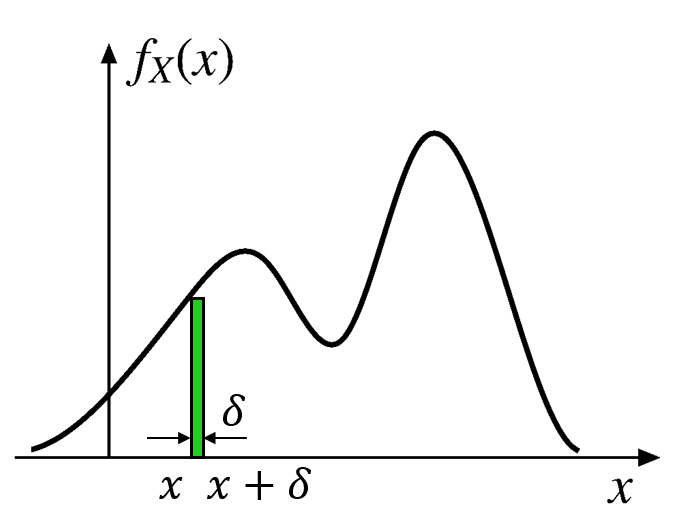
\small{\text{P}([x, x+\delta])=\int_x^{x+\delta} f_X(t)dt \approx f_X(x) \cdot \delta}
\]
\[
\small{f_X(x) \approx \frac{\text{P}([x, x+\delta])}{\delta}}
\]
\(f_X\) is the probability mass per unit length.
Properties of PDF
\[
\text{P}(a \leq X \leq b)=\int_a^b f_X dx
\]
Non-negativity:
As probability can not be negative, we have
\[
f_X(x) \geq 0, \;\; \text{for all $x$.}
\]
Properties of PDF
\[
\text{P}(a \leq X \leq b)=\int_a^b f_X dx
\]
Set \(b=a\), we have
\[
\begin{aligned}
\text{P}(a \leq X \leq a)&=\int_a^a f_X dx=0 \\
\\
\text{P}(X = a)&=0
\end{aligned}
\]
The prob. that a continuous RV takes any single value is 0.
Properties of PDF
\[
\text{P}(X = a)=0
\]
Implication: Including or excluding the endpoints of an interval has no effect on its probability.
\[
\begin{aligned}
\text{P}(a \leq X \leq b)&=\text{P}(a < X \leq b) \\
\\
&=\text{P}(a \leq X < b) \\
\\
&=\text{P}(a < X < b) \\
\end{aligned}
\]
Properties of PDF
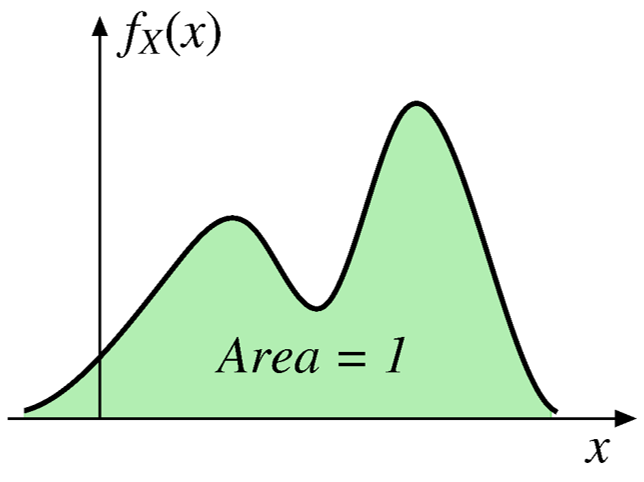
Normalization: For any discrete RV, we have \(\sum_{x} p_X(x) = 1\)
For any continuous RV, we have \[
\text{P}(-\infty < X < +\infty)=\int_{-\infty}^{+\infty} f_X dx=1
\]
Common derivatives
\[
\begin{aligned}
\frac{d}{dx}(c)&=0 \\
\\
\frac{d}{dx}(kx)&=k \\
\\
\frac{d}{dx}(x^n)&=nx^{n-1} \\
\end{aligned}
\]
\[
\begin{aligned}
\frac{d}{dx}(\ln x)&=\frac{1}{x} \\
\\
\frac{d}{dx}(e^x)&=e^x \\
\\
\frac{d}{dx}(a^x)&=a^x \ln(a) \\
\end{aligned}
\]
Common integrals
\[
\small{
\begin{aligned}
&\int k\;dx=kx+c \\
\\
&\int x^n dx=\frac{x^{n+1}}{n+1}+c, \;\;n \neq -1 \\
\\
&\int \frac{1}{x}dx=\ln |x|+c \\
\end{aligned}
}
\]
\[
\small{
\begin{aligned}
&\int e^x dx=e^x+c \\
\\
&\int a^x dx=\frac{a^x}{\ln a}+c \\
\end{aligned}
}
\]
Chain rule
\[
\frac{d}{dx}\bigg(f\big(g(x)\big)\bigg)=f'\big(g(x)\big)\cdot g'(x)
\]
Fundamental theorem of calculus
\[
\int_a^b f(x)dx=F(x)\bigg|_a ^b=F(b)-F(a)
\]
\[
\text{where $F(x)$ is any antiderivative of $f(x)$.}
\]
