3.9 Geometric distribution
- Keep tossing a coin. At each toss
- it lands on a heads with probability of \(p\)
- it lands on a tails with probability of \(1-p\).
\(X\): the number of tosses needed to see the first heads
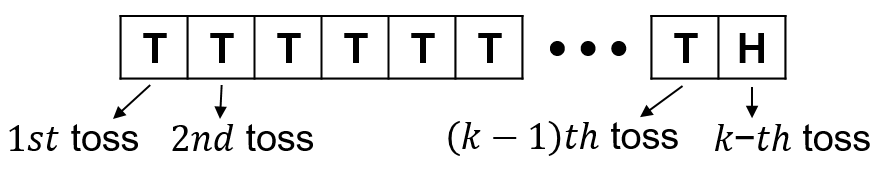
We refer to \(X\) as a geometric RV with parameter \(p\).
\[ X \sim \text{geo}(p) \]

\[ p_X(k)=\text{P}(X=k)=(1-p)^{k-1}p, \;\;\;\;\;\;\text{for } k=1, 2, \cdots \]
It can also be written as:
\[ \begin{aligned} p_X(1)&=p \\ p_X(k)&=p_X(k-1)\cdot(1-p),\;\;\;\;\;\;\text{for } k=2, 3, \cdots \\ \end{aligned} \]
With a common ratio of \((1-p)\), the PMF follows a geometric sequence, hence the name of the RV.
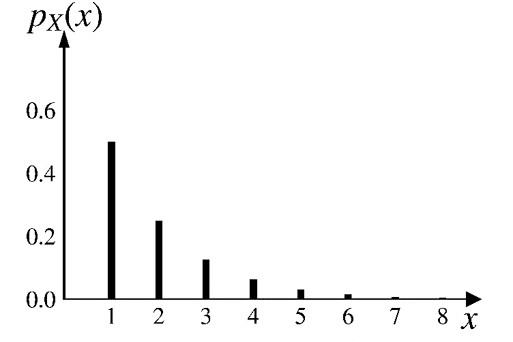
\(\text{geo}(0.5)\;\;\;\)
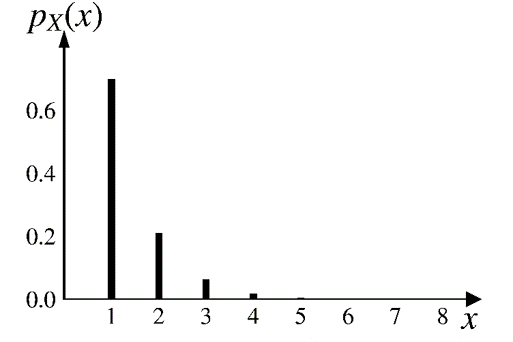
\(\text{geo}(0.7)\;\;\;\)
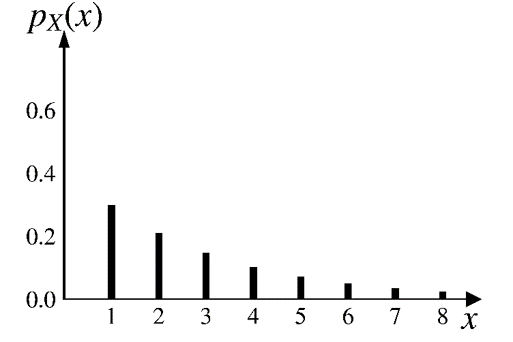
\(\text{geo}(0.3)\;\;\;\)
Interactive visualization
CDF
\[ \small{ \begin{aligned} F_X(k)=\text{P}(X\leq k)&=\sum_{i=1}^k (1-p)^{i-1}p \\ &=p\cdot\frac{1-(1-p)^k}{1-(1-p)} \\ &=1-(1-p)^k \\ \end{aligned} } \]
\[ \small{ \begin{aligned} \text{An easier proof:} \; F_X(k)=\text{P}(X\leq k)&=1-\text{P}(X>k) \\ &=1-\text{P}(\text{all $k$ tosses are tails})\\ &=1-(1-p)^k \\ \end{aligned} } \]
Expectation & variance
\[ p_X(k)=\text{P}(X=k)=(1-p)^{k-1}p, \;\;\;\;\;\text{for } k=1, 2, \cdots \]
\[
\begin{aligned}
\text{E}[X]&=\sum_{k=1}^{\infty} k (1-p)^{k-1}p = \frac{1}{p} \\
\\
\text{var}(X)&=\text{E}[X^2]-\big(\text{E}[X]\big)^2=\frac{1-p}{p^2} \\
\end{aligned}
\]
Gambler’s fallacy
Memoryless property
Given that a coin has been tossed \(t\) times with all tails, the probability of needing more than another \(s\) tosses to see the first heads, is the same as the probability of simply needing more than \(s\) tosses to see the first heads originally.
\[\small{ \text{P}(X>t+s|X>t)=\text{P}(X>s) \\ \text{for all nonnegative integers $t$ and $s$} }\]
It’s called memoryless because the past (the last \(t\) coin toss were all tails) has no bearing on its future (the probability of needing at least \(s\) more tosses before seeing the first heads).
\[ \small{ \begin{aligned} \text{P}(X>t+s|X>t)&=\frac{\text{P}\big((X>t+s) \cap (X>t)\big)}{\text{P}(X>t)} \\ \\ &=\frac{\text{P}(X>t+s)}{\text{P}(X>t)} \\ \\ &=\frac{(1-p)^{t+s}}{(1-p)^t} \\ \\ &=(1-p)^s =\text{P}(X>s) \\ \end{aligned} } \]