3.6 Uniform distribution

Discrete uniform random variable

\(X\): Roll a die 🎲 and record the roll

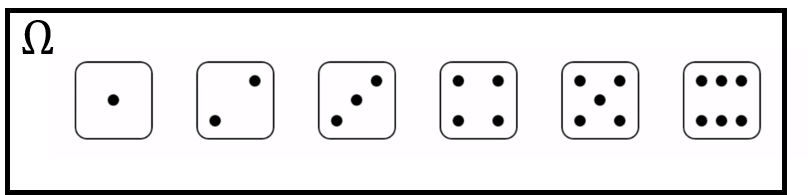
\[p_X(x) = \begin{cases} 1/6, & \text{if } x = 1, 2, \cdots, 6, \\ 0, & \text{otherwise.} \end{cases} \]

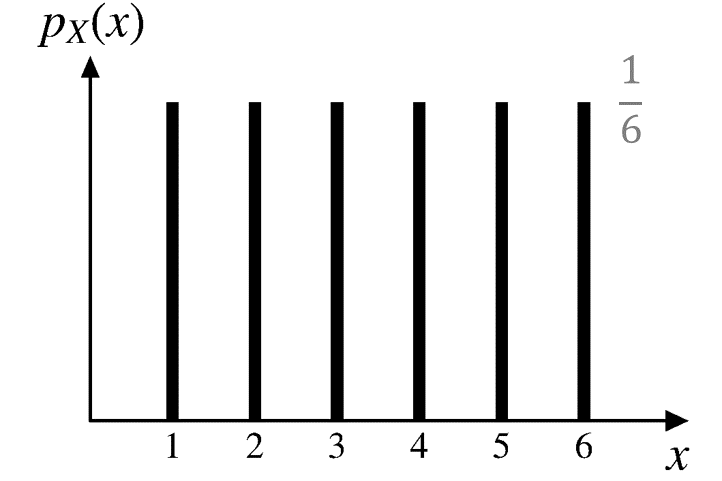
Discrete uniform RV

A discrete uniform RV takes one out of a range of contiguous integer values, with equal probability.

\[ p_X(k) = \begin{cases} \frac{1}{b-a+1}, & \text{if } k = a, a+1, \cdots, b, \\ 0, & \text{otherwise.} \\ \end{cases} \]

\[ \text{where $a$ and $b$ are two integers with $a < b$} \]

Discrete uniform RV

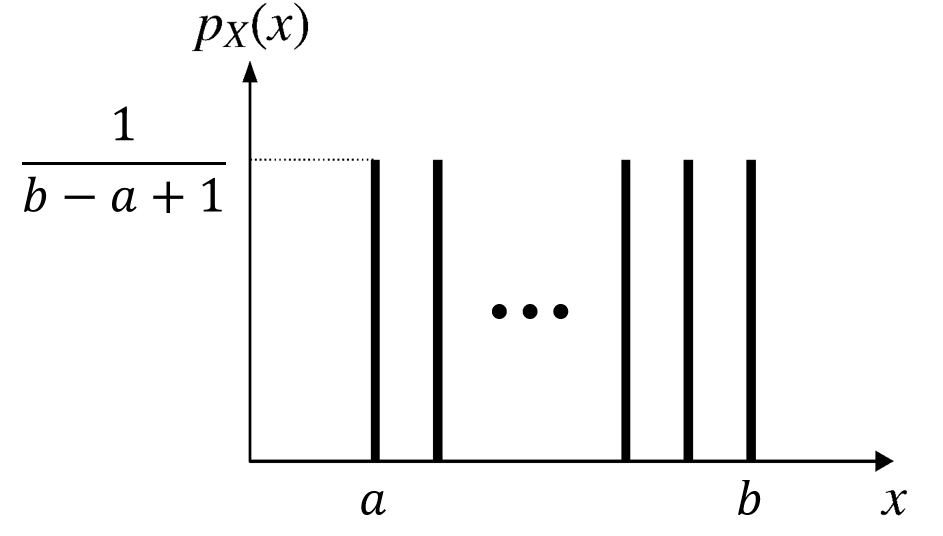
\(X\) is a discrete uniform RV with parameters \(a\) and \(b\).

\[ X\sim\text{unif}\{a, b\} \]

It is a family of all discrete uniform distributions for different values of \(a\) and \(b\).

Interactive visualization

Expected value

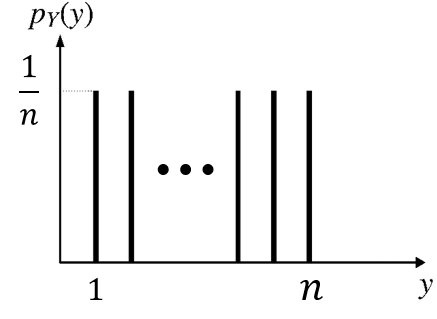
\[ \small{ p_X(k) = \begin{cases} 1/n, & \text{if } k = a, a+1, \cdots, b, \\ 0, & \text{otherwise.} \\ \end{cases} \;\;\text{where $n=b-a+1$ } } \]

\[ \small{ \begin{aligned} \text{E}[X]=\;&\frac{1}{n}\cdot a+\frac{1}{n} \cdot (a+1)+ \cdots+\frac{1}{n} \cdot b \\ =\;&\frac{1}{n} \cdot \big[a+(a+1)+\cdots+b\big] \\ % &\color{lightgray}{\text{Note the 2nd part above is an arithmetic series.}}\\ =\;&\frac{1}{n} \cdot \frac{n(a+b)}{2} \\ =\;&\frac{a+b}{2} \\ \end{aligned} } \]

Variance

\[ p_X(k) = \begin{cases} 1/n, & \text{if } k = a, a+1, \cdots, b, \\ 0, & \text{otherwise.} \\ \end{cases} \;\;\text{where $n=b-a+1$ } \]

\[ \text{Let }Y=X-a+1 \]

\[ \text{var}(Y)=\text{var}(X-a+1)=\text{var}(X) \]

\[ \small{\text{var}(Y)=\text{E}\big[Y^2\big]-\big(\text{E}[Y]\big)^2} \]

\[ \small{ \begin{aligned} \text{E}[Y]&=\frac{n+1}{2} \\ \text{E}\big[Y^2\big]&=\sum_{k=1}^n \big(k^2 \frac{1}{n} \big)\\ &=\frac{1}{n}\color{gray}{\sum_{k=1}^nk^2} \;\;\;\;\; \color{gray}{\leftarrow\text{Square pyramidal number}}\\ &=\frac{1}{6}(n+1)(2n+1) \\ \end{aligned} } \]

Lastly,

\[ \begin{aligned} \text{var}(Y)&=\text{E}\big[Y^2\big]-\big(\text{E}[Y]\big)^2 \\ \\ &=\frac{1}{6}(n+1)(2n+1)-\big(\frac{n+1}{2}\big)^2 \\ \\ &=\frac{n^2-1}{12} \\ \end{aligned} \]

\[ X\sim\text{unif}\{a, b\} \]

\[ \begin{aligned} \text{E}[X]&=\frac{a+b}{2} \\ \\ \text{var}(X)&=\frac{n^2-1}{12} \;\;\;\text{where } n=b-a+1 \end{aligned} \]