3.5 Variance
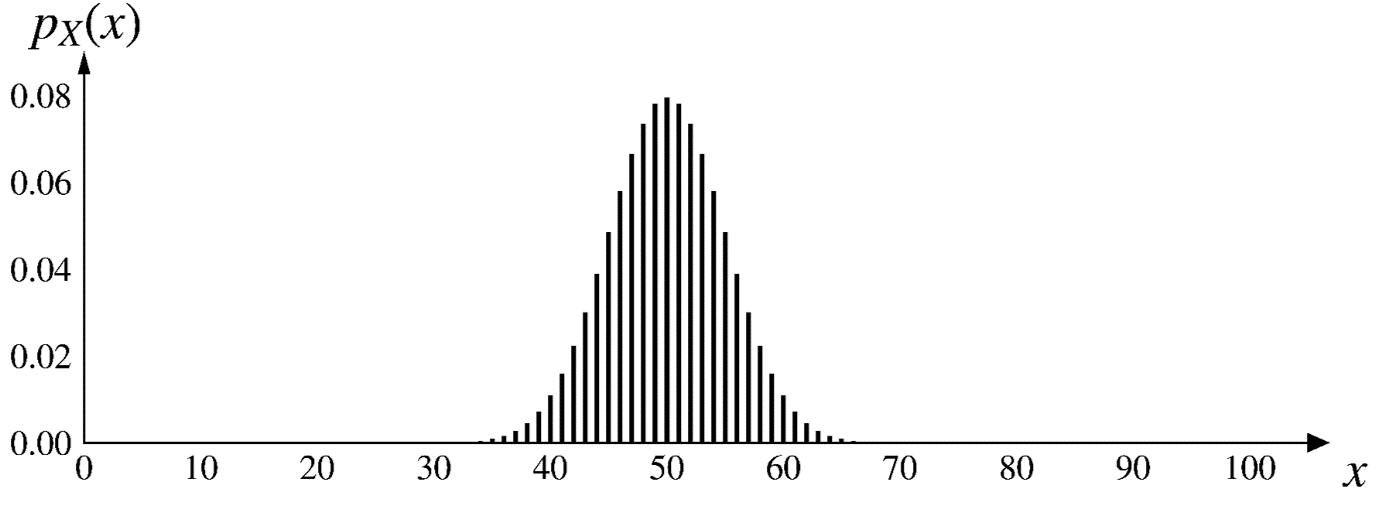
The expected value gives the center of an distribution.
\[\text{E}[X]=50\]
How can we measure the spread of the distribution?
Variance
The variance of a RV \(X\), denoted by \(\text{var}(X)\) or \(\sigma_X^2\), is defined by
\[ \text{var}(X)=\text{E}\bigg[\big(X-\text{E}[X]\big)^2\bigg] \]
How to compute the variance
\[ \text{var}(X)=\text{E}\bigg[\big(X-\text{E}[X]\big)^2\bigg] \]
\[ \text{Let }g(X)=\big(X-\text{E}[X]\big)^2 \]
By LOTUS, the variance can be calculated as
\[ \text{var}(X)=\text{E}\big[g(X)\big]=\sum_x \bigg[\big(x-\text{E}[X]\big)^2 \cdot p_X(x) \bigg] \]
Standard deviation
The square root of the variance, denoted by \(\sigma_X\), is called the standard deviation.
\[\sigma_X=\sqrt{\sigma_X^2}\]
Variance of a linear function of a RV
For any given constants \(a\) and \(b\), we have
\[ \text{var}(aX+b)=a^2 \text{var}(X) \]
Proof
\[ \begin{aligned} \text{var}(aX+b)&=\sum_x (ax+b-\text{E}[aX+b])^2 \cdot p_X(x) \\ &=\sum_x (ax+b-(a\text{E}[X]+b))^2 \cdot p_X(x) \\ &=a^2\sum_x (x-\text{E}[X])^2 \cdot p_X(x) \\ &=a^2 \text{var}(X) \end{aligned} \]
A shortcut for finding variance
\[\text{var}(X)=\text{E}[X^2]-\big(\text{E}[X]\big)^2\]
Proof
\[ \begin{aligned} &\text{var}(X)\\ =\;&\sum_x (x-\text{E}[X])^2 \cdot p_X(x) \;\;\;\;\; \color{gray}{\leftarrow\text{by LOTUS}} \\ =\;&\sum_x (x^2-2x\text{E}[X]+(\text{E}[X])^2) \cdot p_X(x) \\ =\;&\sum_x x^2 \cdot p_X(x) -2\text{E}[X]\sum_x x \cdot p_X(x) + (\text{E}[X])^2\sum_x p_X(x) \\ =\;&\text{E}[X^2] -2(\text{E}[X])^2 + (\text{E}[X])^2 \\ =\;&\text{E}[X^2]-(\text{E}[X])^2 \\ \end{aligned} \]