Probability mass function of a RV \(X\)
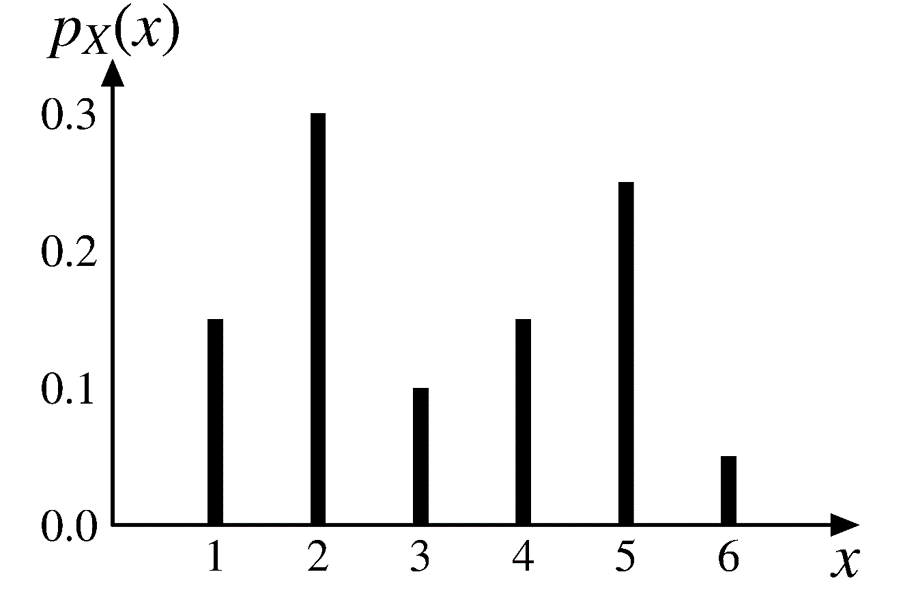
What is a single representative value for \(X\)?
The expected value of a discrete RV \(X\) is defined by
\[
\text{E}[X]=\sum_x x \cdot p_X(x)
\]
It’s the probability-weighted average of all values of \(X\).
It measures the center of the distribution.
What is the expected value of \(X\)?
\[
\small{
p_X(x) =
\begin{cases}
0.15, & \text{if $x = 1$,} \\
0.30, & \text{if $x = 2$,} \\
0.10, & \text{if $x = 3$,} \\
0.15, & \text{if $x = 4$,} \\
0.25, & \text{if $x = 5$,} \\
0.05, & \text{if $x = 6$,} \\
0, & \text{otherwise.}
\end{cases}
}
\]
\[
\small{
\begin{aligned}
\text{E}[X]=&\; 1 \cdot p_X(1) + 2\cdot p_X(2) + \cdots + 5 \cdot p_X(5) + 6 \cdot p_X(6) \\
=&\; 1 \cdot 0.15 + 2 \cdot 0.30 + \cdots + 5 \cdot 0.25 + 6 \cdot 0.05 \\
=&\; 3.2 \\
\end{aligned}
}
\]
- \(X\): Roll a fair die 🎲 and record the number
- What is the expected value of \(X\)?
\[
\small{
p_X(x) =
\begin{cases}
1/6, & \text{if } x = 1, 2, \cdots, 6, \\
0, & \text{otherwise.}
\end{cases}
}
\]
\[
\begin{aligned}
\text{E}[X]&=1\cdot\frac{1}{6}+2\cdot\frac{1}{6}+3\cdot\frac{1}{6}+4\cdot\frac{1}{6}+5\cdot\frac{1}{6}+6\cdot\frac{1}{6} \\\
&=3.5
\end{aligned}
\]
\[
\small{
p_X(x) =
\begin{cases}
1/6, & \text{if } x = 1, 2, \cdots, 6, \\
0, & \text{otherwise.}
\end{cases}
}
\]
\[
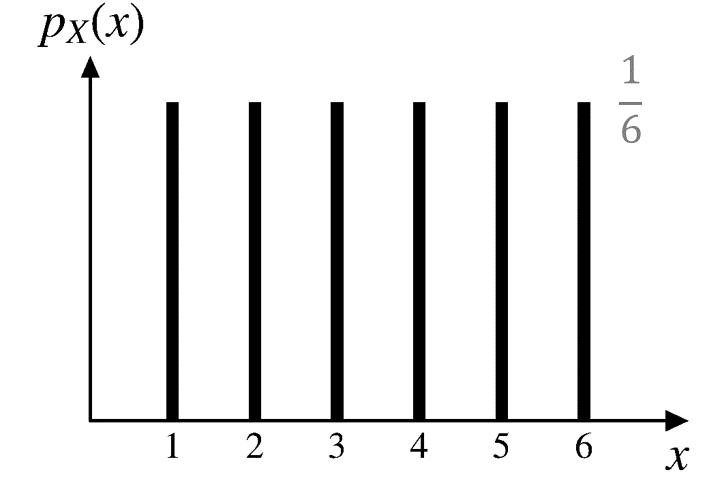
\text{E}[X]=3.5
\]
If the PMF is symmetrical, \(\text{E}[X]\) is at the middle point.
Exercise
- A lottery ticket offers
- 1 in 500 chance to win $1,000
- 1 in 10 chance to win $10
- otherwise, you win nothing.
- If the lottery ticket costs $2 each, should you buy it?
- \(X\): The amount of money you win with one ticket.
- What is the expected value of \(X\)?
Extended Warranty
- Assume during the coverage of the extended warranty, the laptop will break with the following probabilities:
- Zero times (65%), once (20%), twice (10%), 3 times (5%)
- Each break would cost $200 to repair.
- Should you buy this extended warranty?
- \(X\): The amount of money you pay for repair without buying the warranty
- What is the expected value of \(X\)?
![]()
What is Osifo’s expected points at the free throw line?
Expected value of a function of a RV
\[
\small{
\text{PMF of a RV $X$: }
p_X(x) =
\begin{cases}
1/5, & \text{if $x = -2, -1, 0, 1, 2$,} \\
0, & \text{otherwise.}
\end{cases}
}
\]
What is the expected value of \(Y=|X|\)?
\[
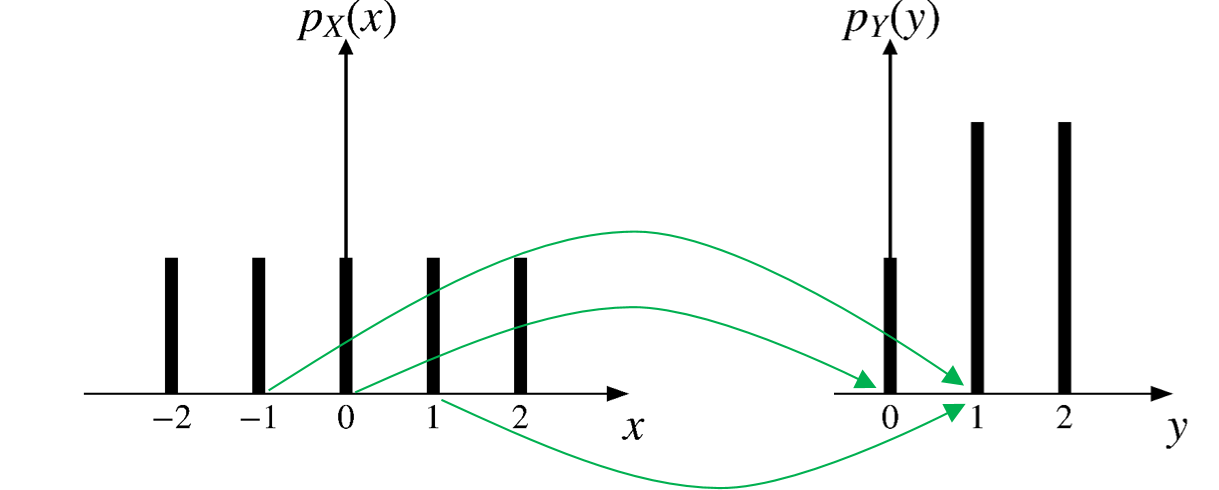
\small{
p_Y(y) =
\begin{cases}
2/5, & \text{if $y = 1, 2$,} \\
1/5, & \text{if $y = 0$,} \\
0, & \text{otherwise.}
\end{cases}
}
\]
Can we get \(\text{E}[Y]\) directly using the PMF of \(X\), rather than having to first calculating the PMF of \(Y=|X|\)?
\[p_X(x) =
\begin{cases}
1/5, & \text{if $x = -2, -1, 0, 1, 2$,} \\
0, & \text{otherwise.}
\end{cases}
\]
\[Y=|X|\]
What is the expected value of \(Y\)?
\[
\small{
\begin{aligned}
\text{E}[Y]&=\sum_y \big[y \cdot p_Y(y)\big] \;\;\;\;\;\; \color{gray}{\leftarrow\text{by definition of expected value}} \\
&=\sum_y \bigg[y \cdot \sum_{\\{x|g(x)=y\\}}p_X(x)\bigg] \\
&=\sum_y \bigg[\sum_{\\{x|g(x)=y\\}} y \cdot p_X(x) \bigg] \\
&=\sum_y \bigg[\sum_{\\{x|g(x)=y\\}} g(x) \cdot p_X(x) \bigg]
=\sum_x \big[g(x) \cdot p_X(x) \big] \\
\end{aligned}
}
\]
Linearity of the expected value
For any given constants \(a\) and \(b\), we have
\[
\text{E}[aX+b]=a \text{E}[X] + b
\]
\[
\begin{aligned}
\text{Proof:} \;\;
\text{E}[aX+b]&=\sum_x \big[(ax+b) \cdot p_X(x)\big] \;\;\;\;\; \color{gray}{\leftarrow\text{by LOTUS}} \\
&=\sum_x \big[ ax \cdot p_X(x) + b \cdot p_X(x)\big] \\
&=a\sum_x \big[x \cdot p_X(x) \big] + b \sum_x p_X(x) \\
&=a\text{E}[X]+b \\
\end{aligned}
\]
Linearity of the expected value
\[
\text{E}[aX+b]=a \text{E}[X] + b
\]
That is, when \(g(X)\) is a linear function, we have
\[
\text{E}\big[g(X)\big]=g\big(\text{E}[X]\big)
\]
\[
\text{E}\big[g(X)\big]=g\big(\text{E}[X]\big)
\]
\[
\text{Celcius}=(\text{Farenheit}-32) \cdot \frac{5}{9}
\]
If we already know \(\text{E[Farenheit]}=41\), then
\[
\text{E[Celcius]}=(\text{E[Farenheit]}-32) \cdot \frac{5}{9}=(41-32) \cdot \frac{5}{9}=5
\]
However, in general,
\[
\text{E}\big[g(X)\big] \neq g\big(\text{E}[X]\big)
\]
Example
- Sarah lives 2 miles away from the campus.
- She walks to classes at 4 mph if the weather is good (assuming that is half of the time).
- Otherwise, she cycles to classes at a speed of 20 mph.
- What is the expected
- travel speed?
- travel time?
Travel speed \(V\)
\[
\begin{aligned}
p_V(v) &=
\begin{cases}
0.5, & \text{if $v=4$ or 20 mph,} \\
0, & \text{otherwise.} \\
\end{cases}
\end{aligned}
\]
\[ \text{E}[V] = 4 \cdot 0.5 + 20 \cdot 0.5 = 12 \text{ (mph)}
\]
Travel time \(T\)
\[
T=g(V)=\frac{\text{distance}}{V}=\frac{2}{V}
\]
\[
\small{
\begin{aligned}
t &=
\begin{cases}
2 / 4 =0.5, & \text{if walking,} \\
2 / 20 =0.1, & \text{if cycling.} \\
\end{cases}
\end{aligned}
}
\]
\[
\small{
\begin{aligned}
p_T(t) &=
\begin{cases}
0.5, & \text{if $t=0.1$ or 0.5 hours,} \\
0, & \text{otherwise.} \\
\end{cases}
\end{aligned}
}
\]
Travel time \(T\) (cont’d)
\[
\small{
\begin{aligned}
p_T(t) &=
\begin{cases}
0.5, & \text{if $t=0.1$ or 0.5 hours,} \\
0, & \text{otherwise.} \\
\end{cases}
\end{aligned}
}
\]
\[
\small{\color{gray}{\big(\text{E}\big[g(V)\big]=\big)} \;\; \text{E}[T] = 0.1 \cdot 0.5 + 0.5 \cdot 0.5 = 0.3 \text{ (hours)}}
\]
\[
\small{g\big(\text{E}[V]\big)=\frac{2}{\text{E}[V]}=\frac{2}{12}\approx0.167}
\]
\[
\small{\text{E}\big[g(V)\big] \neq g\big(\text{E}[V]\big)}
\]
