3.3 Cumulative Distribution Function

Cumulative Distribution Function (CDF)

The CDF of a RV \(X\) is defined by

\[F_X(x)=\text{P}(X \leq x), \;\text{for all $x$.}\]

• It is the probability that the value of \(X\) is at most \(x\).
• Loosely speaking, the CDF accumulates the probability up to the value \(x\).
• If RV \(X\) is discrete, \[F_X(x)=\text{P}(X \leq x)=\sum_{k \leq x} p_X(k)\]

Finding CDF

• \(X\): Roll a die 🎲 and record the number
• What is the CDF of \(X\)?

\[F_X(x)=\text{P}(X \leq x), \;\text{for all $x$.}\]

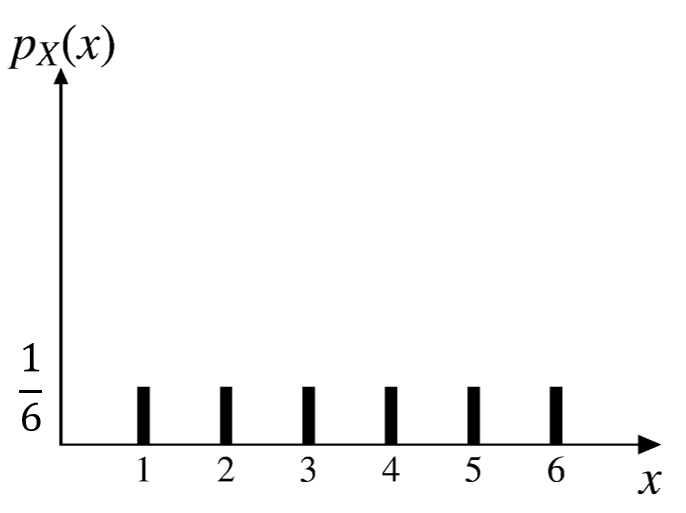
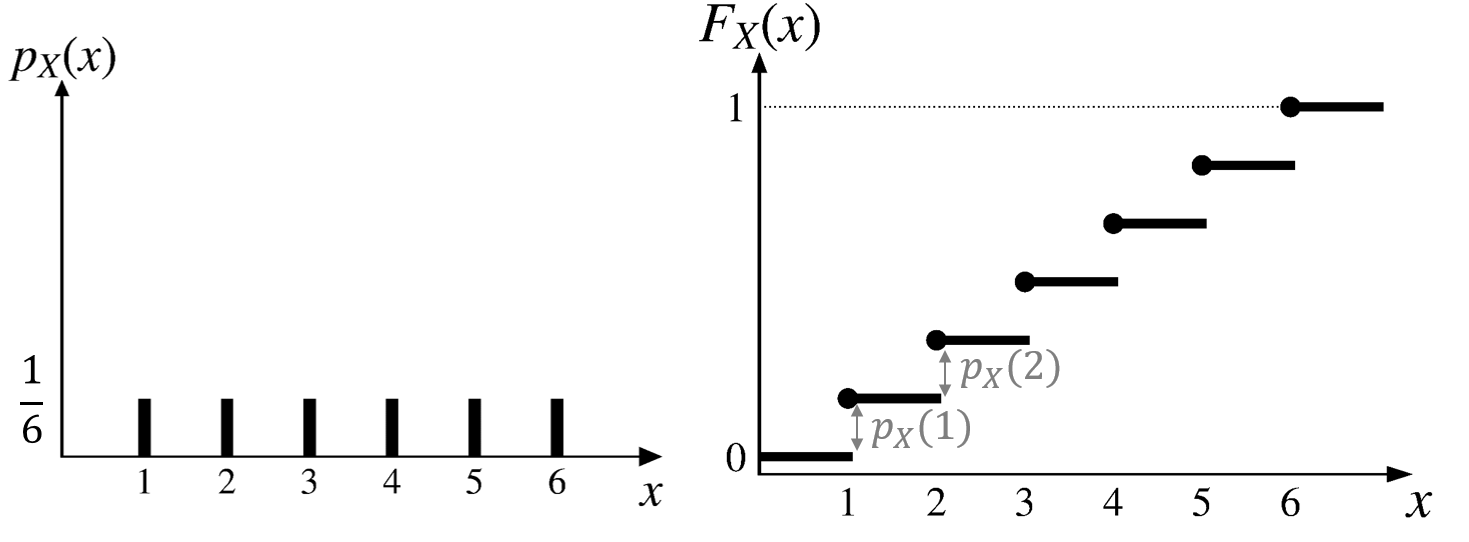
For discrete RVs the CDF \(F_X(x)\) is a step function of \(x\).

\[ \small{ F_X(x) = \begin{cases} 0, & \text{if $ x < 1$,} \\ 1/6, & \text{if } 1 \leq x < 2, \\ 2/6, & \text{if } 2 \leq x < 3, \\ 3/6, & \text{if } 3 \leq x < 4, \\ 4/6, & \text{if } 4 \leq x < 5, \\ 5/6, & \text{if } 5 \leq x < 6, \\ 1, & \text{if } x \geq 6. \\ \end{cases} } \]

• \(X\): Toss a coin twice and record the number of heads.
• What is the CDF of \(X\)?

\[ \small{ p_X(x) = \begin{cases} 0.25, & \text{if $x = 0$ or 2}, \\ 0.5, & \text{if $x = 1$,} \\ 0, & \text{otherwise.} \end{cases} } \]

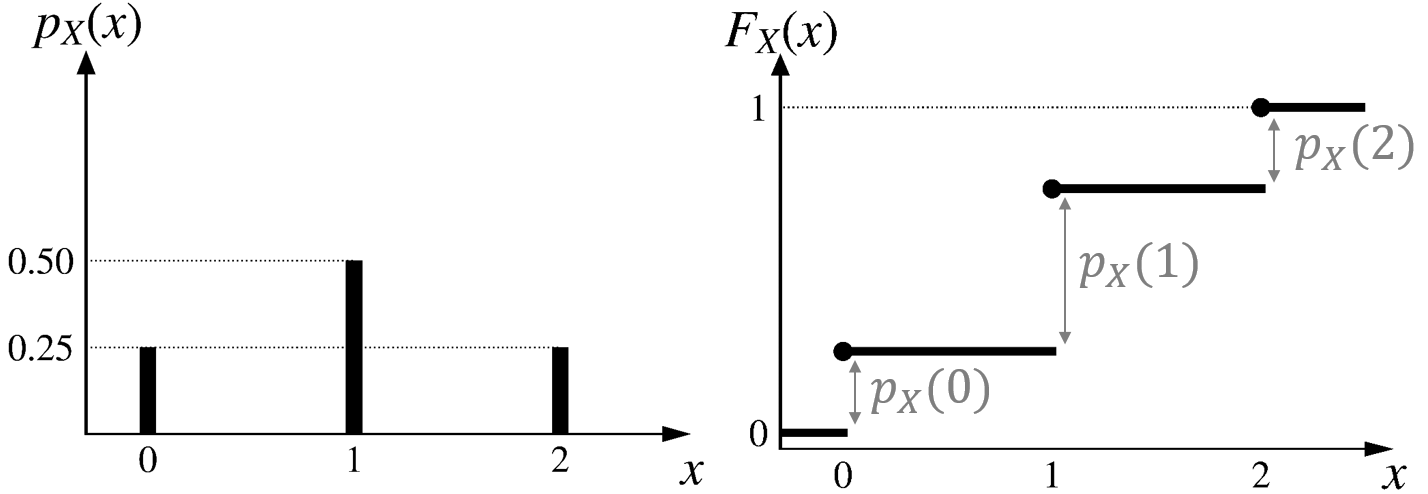
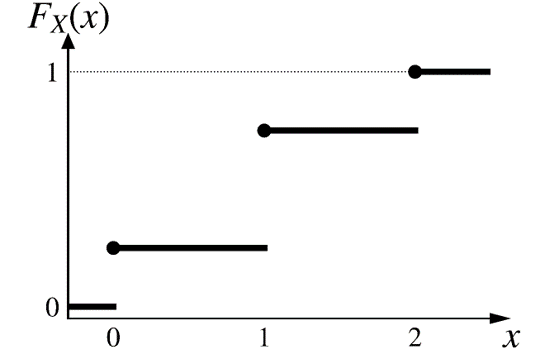
\[ \small{ F_X(x) = \begin{cases} 0, & \text{if $x < 0$,} \\ 0.25, & \text{if } 0 \leq x < 1, \\ 0.75, & \text{if } 1 \leq x < 2, \\ 1, & \text{if } x \geq 2. \\ \end{cases} } \]

If \(X\) only takes integer values, its PMF can be obtained from CDF by differencing.

\[ \small{ p_X(k)=\text{P}(X \leq k) - \text{P}(X \leq k-1) = F_X(k) - F_X(k-1)\\ } \]

\[ \small{ \begin{aligned} p_X(0)&=F_X(0)-F_X(-1)=0.25-0=0.25 \\ p_X(1)&=F_X(1)-F_X(0)=0.75-0.25=0.5 \\ p_X(2)&=F_X(2)-F_X(1)=1-0.75=0.25 \\ \end{aligned} } \]

Properties of CDF

A CDF is nondecreasing.

\[ % \begin{aligned} \text{If } a \leq b, \text{then } F_X(a) \leq F_X(b). % \\ % \text{then } F_X(a) &\leq F_X(b). % \end{aligned} \]

\(F_X(x)\) tends to \(0\) as \(x\rightarrow -\infty\), and to \(1\) as \(x \rightarrow +\infty\).