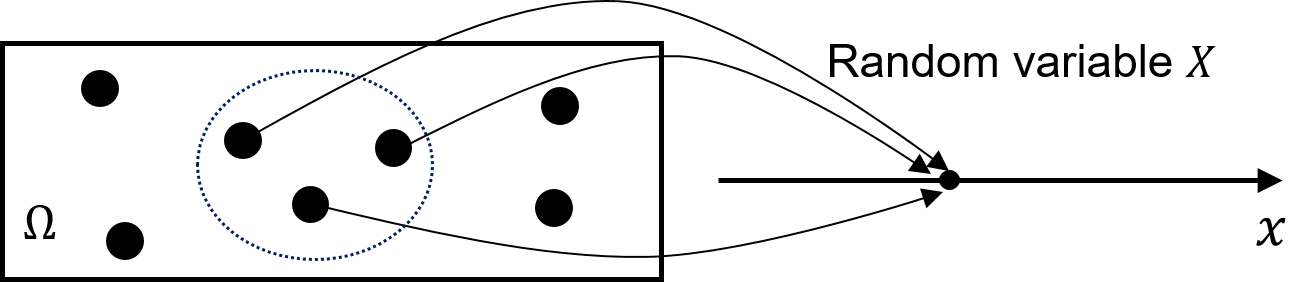
3.2 Probability mass function

Some notations

By convention, we use

• upper case letters (e.g., \(X\)) to denote RV’s.
• lower case letters (e.g., \(x\)) to denote any specific value that a RV can take.

\(X=x\) represents the event that RV \(X\) takes value \(x\).

Probability Mass Function (PMF)

The PMF of a discrete RV \(X\) is defined by

\[ \begin{aligned} p_X(x) =& \; \text{P}(X=x) \\ =& \; \text{P}(\text{all outcomes in $\Omega$ that give rise to $X=x$)} \\ \text{for all $x$.}& \\ \end{aligned} \]

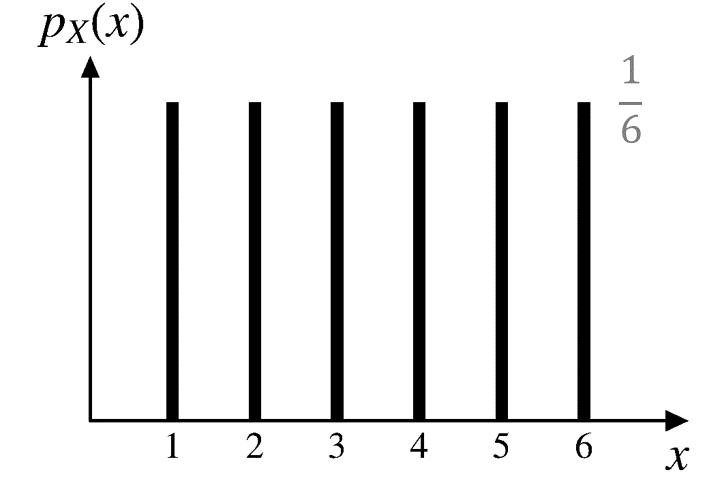
Example

\(X\): Roll a die and record the number

\[ \begin{aligned} p_X(1) &= \text{P}(X=1)= \text{P}(⚀)=1/6 \\ p_X(2) &= \text{P}(X=2)= \text{P}(⚁)=1/6 \\ &\cdots \\ p_X(6) &= \text{P}(X=6)= \text{P}(⚅)=1/6 \\ \end{aligned} \]

Example (cont’d)

More compactly, we can write the PMF as

\[p_X(x) = \begin{cases} 1/6, & \text{if } x = 1, 2, \cdots, 6, \\ 0, & \text{otherwise.} \end{cases} \]

Find the PMF of \(X\)

\(X\): Toss a coin twice and record the number of heads.

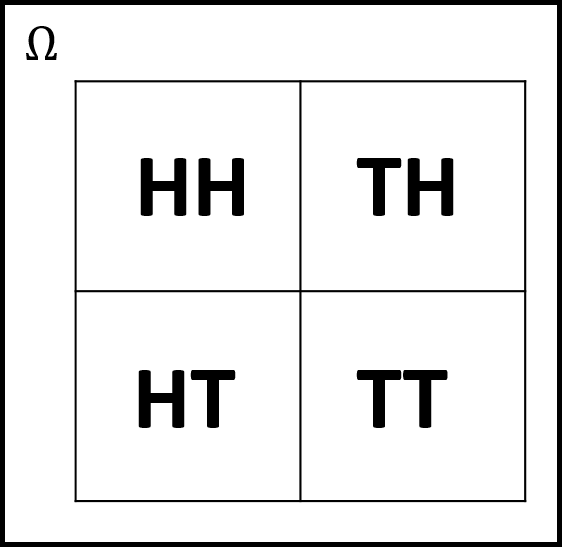
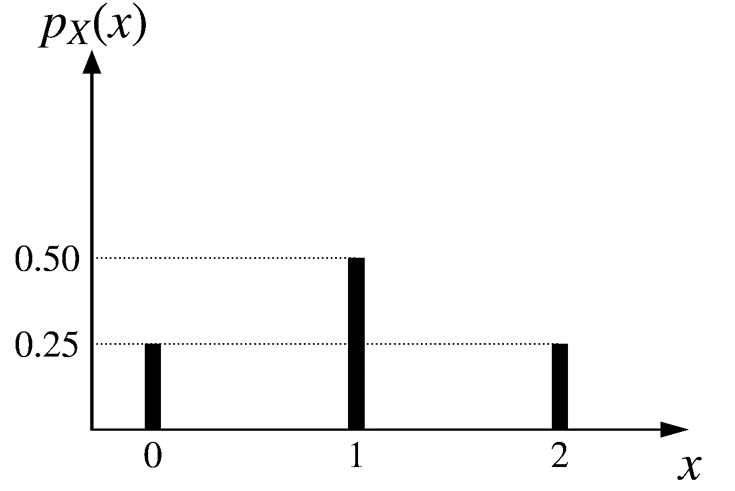
Find the PMF of \(X\)

\(X\): Toss a coin twice and record the number of heads.

\[p_X(x) = \begin{cases} 1/4, & \text{if $x = 0$ or 2,} \\ 1/2, & \text{if $x = 1$,} \\ 0, & \text{otherwise.} \end{cases} \]

Find the PMF of \(X\)

\(X\): Roll a pair of dice 🎲 🎲 and record the max roll.

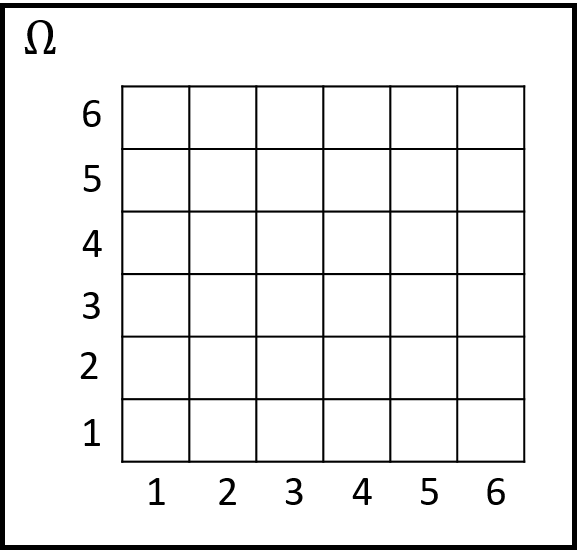
Find the PMF of \(X\)

\(X\): Roll a pair of dice and record the maximum roll.

Procedure of finding the PMF of a RV

\[ \begin{aligned} p_X(x) =& \; \text{P}(X=x) \\ =& \; \text{P}(\text{all outcomes in $\Omega$ that give rise to $X=x$}) \\ \text{for all $x$.}& \\ \end{aligned} \]

1. List all possible values of \(x\) that the RV \(X\) can take.
2. For each \(x\),
   • collect all the possible outcomes that give rise to the event \(\{X=x\}\)
   • add their probabilities to obtain \(p_X(x)\)

Properties of PMF

For any RV \(X\)

\[p_X(x) \geq 0, \;\;\;\; \text{for any $x$.}\]

For any RV \(X\)

\[\sum_x p_X(x) = 1\]

\[\text{where $x$ ranges over all possible values of $X$.}\]

Functions of random variables

\[\large{p_Y(y)=\sum_{\\{x|g(x)=y\\}}p_X(x)}\]

Exercise

RV \(X\) has the following PMF:

\[p_X(x) = \begin{cases} 1/5, & \text{if $x = -2, -1, 0, 1, 2$,} \\ 0, & \text{otherwise.} \end{cases} \]

RV \(Y\) is defined as

\[Y=|X|\]

What is the PMF of \(Y\)?

\[p_X(x) = \begin{cases} 1/5, & \text{if $x = -2, -1, 0, 1, 2$,} \\ 0, & \text{otherwise.} \end{cases} \]

\[Y=|X|\]

\[p_Y(y)=\sum_{\\{x|g(x)=y\\}}p_X(x)\]

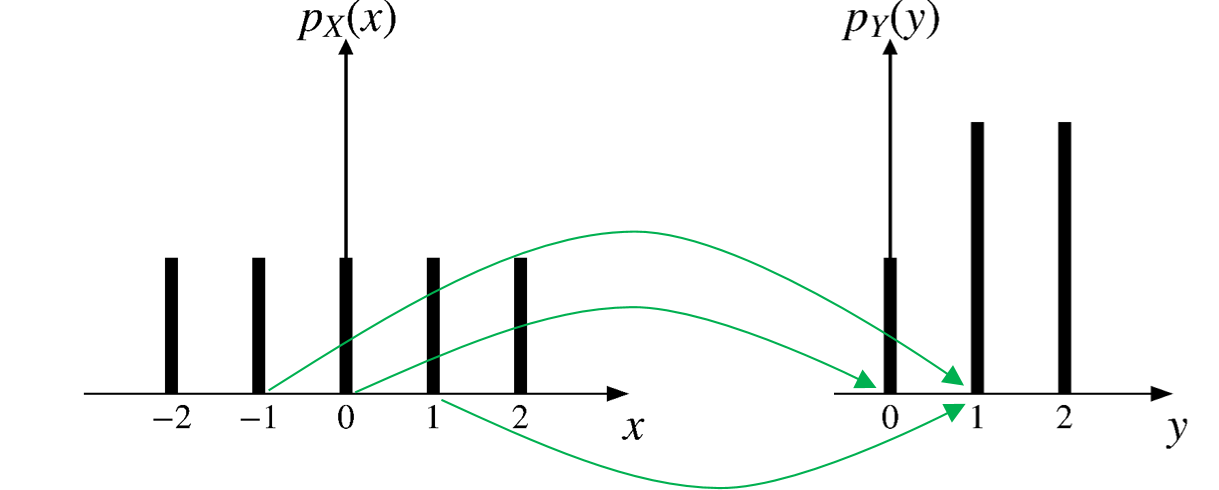
\[p_Y(y) = \begin{cases} 2/5, & \text{if $y = 1, 2$,} \\ 1/5, & \text{if $y = 0$,} \\ 0, & \text{otherwise.} \end{cases} \]