2.11 Independence


Event \(A\) is independent of event \(B\) if
\[ \text{P}(A \mid B)=\text{P}(A) \]
By the definition of conditional probability,
\[ \text{P}(A \mid B) = \frac{\text{P}(A \cap B)}{\text{P}(B)} \]
From the two equation above, we have
\[ \text{P}(A) = \frac{\text{P}(A \cap B)}{\text{P}(B)} \]
\[ \text{P}(A \cap B) = \text{P}(A) \cdot \text{P}(B) \]
Exercise
- Roll a die twice 🎲 🎲
- \(A\): the first roll lands on \(3\).
- \(B\): the second roll lands on \(4\).
- Are \(A\) and \(B\) independent?
Properties of independence
If \(A\) and \(B\) are independent, so are \(A\) and \(B^c\).
Intuitively, if knowing that \(B\) has occurred does not provide any new information on how likely \(A\) occurs,
\[ \text{P}(A \mid B)=\text{P}(A) \]
then knowing that the complement of \(B\) has occurred should also provide no information on how likely \(A\) occurs.
\[ \text{P}(A \mid B^c)=\text{P}(A) \]
Are two disjoint events independent?
Independence of three events
- Three events \(A\), \(B\), and \(C\)
- \(A\) and \(B\) are independent.
- \(B\) and \(C\) are independent.
- Are \(A\) and \(C\) independent?
We say events \(A\), \(B\), and \(C\) are pairwise independent if
- \(A\) and \(B\) are independent. \(\text{P}(A \cap B)=\text{P}(A)\cdot\text{P}(B)\)
- \(B\) and \(C\) are independent. \(\text{P}(B \cap C)=\text{P}(B)\cdot\text{P}(C)\)
- \(C\) and \(A\) are independent. \(\text{P}(C \cap A)=\text{P}(C)\cdot\text{P}(A)\)
How about
\[ \text{P}(A \cap B \cap C) \stackrel{?}{=} \text{P}(A)\cdot\text{P}(B)\cdot\text{P}(C) \]
Toss a coin twice
- \(A\): first toss is a heads.
- \(B\): second toss is a heads.
- \(C\): different results from the two tosses.
Are these three events pairwise independent?
Pairwise independence does not imply (mutual) independence.
Independence of three events
Event \(A\), \(B\), and \(C\) are (mutually) independent if
\[ \begin{aligned} \text{P}(A \cap B) &= \text{P}(A)\cdot\text{P}(B) \\ \\ \text{P}(B \cap C) &= \text{P}(B)\cdot\text{P}(C) \\ \\ \text{P}(C \cap A) &= \text{P}(C)\cdot\text{P}(A) \\ \\ \text{P}(A \cap B \cap C) &= \text{P}(A)\cdot\text{P}(B)\cdot\text{P}(C) \\ \end{aligned} \]
Independence of four events
\[ \begin{aligned} \text{P}(A \cap B) &= \text{P}(A)\cdot\text{P}(B) \\ \text{P}(B \cap C) &= \text{P}(B)\cdot\text{P}(C) \\ \text{P}(C \cap D) &= \text{P}(C)\cdot\text{P}(D) \\ \text{P}(D \cap A) &= \text{P}(D)\cdot\text{P}(A) \\ \text{P}(A \cap B \cap C) &= \text{P}(A)\cdot\text{P}(B)\cdot\text{P}(C) \\ \text{P}(A \cap B \cap D) &= \text{P}(A)\cdot\text{P}(B)\cdot\text{P}(D) \\ \text{P}(A \cap C \cap D) &= \text{P}(A)\cdot\text{P}(C)\cdot\text{P}(D) \\ \text{P}(B \cap C \cap D) &= \text{P}(B)\cdot\text{P}(C)\cdot\text{P}(D) \\ \text{P}(A \cap B \cap C \cap D) &= \text{P}(A)\cdot\text{P}(B)\cdot\text{P}(C)\cdot\text{P}(D) \\ \end{aligned} \]
Independence of \(n\) events
Events \(A_1, A_2, \cdots, A_n\) are (mutually) independent if
\[ \text{P}\bigg(\bigcap_{i \in S} A_i\bigg)=\prod_{i \in S} \text{P}(A_i) \]
for every subset \(S\) of \(\{1, 2, \cdots, n\}\).
Example - Network connectivity
- A computer network connects two nodes A and B through 3 components that are connected in series.
![]()
- The component failures are independent of each other.
- \(p_i\) is the probability that component \(i\) is operational (\(i=1, 2, 3\)).
- What is the probability that the A-B connection is up?
- Now, the two nodes A and B through 3 components are connected in parallel.
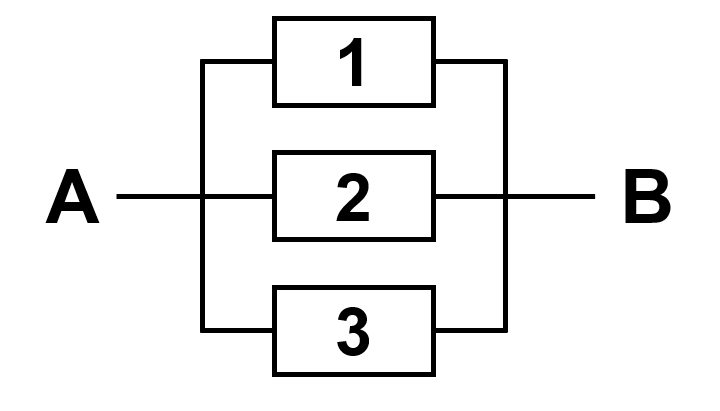
- What is the probability that the A-B connection is up?
