2.9 Total probability theorem

Partition of sample space \(\Omega\)

• If a collection of events are
  • disjoint (i.e., mutually exclusive)
  • their union is \(\Omega\) (i.e., collectively exhaustive)
• then this collection of events is called a partition of \(\Omega\).
• This means any outcome in an experiment is included in one and only one of the partitioning events.

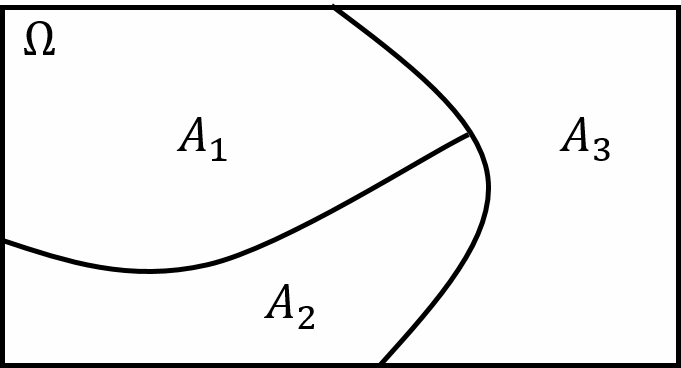
Partition of sample space \(\Omega\)

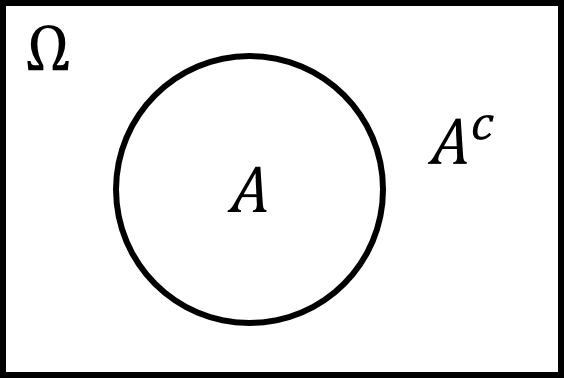
\(A\) and \(A^c\) always form a partition of sample space \(\Omega\).

Total probability theorem

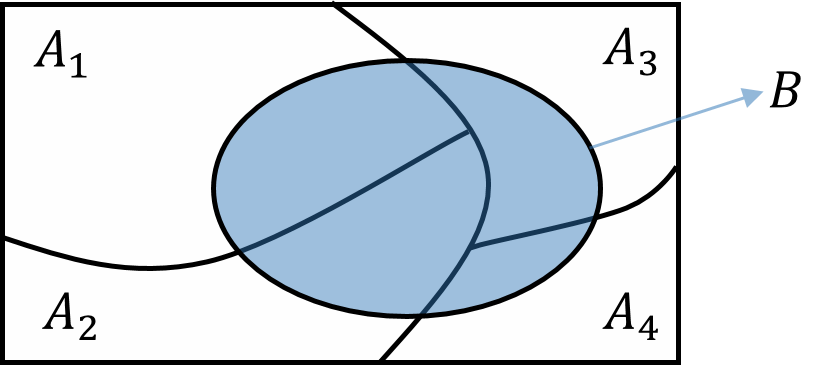
Let \(A_1, A_2, \cdots, A_n\) form a partition of sample space \(\Omega\).

Then, for any event \(B\), we have

\[ B = (A_1 \cap B) \cup (A_2 \cap B) \cup \cdots \cup (A_n \cap B) \]

Exercise

• Your academic department offers
  • 8 lower level courses \(L_1, L_2, \cdots, L_8\)
  • 10 higher level courses \(H_1, H_2, \cdots, H_{10}\)
• A valid curriculum consists of
  • 4 lower level courses
  • 3 higher level courses
• How many different curricula are possible?

Exercise (cont’d)

• Your academic department offers
  • 8 lower level courses \(L_1, L_2, \cdots, L_8\)
  • 10 higher level courses \(H_1, H_2, \cdots, H_{10}\)
• A valid curriculum consists of
  • 4 lower level courses
  • 3 higher level courses

In fact, \(H_1, H_2, \cdots, H_5\) have \(L_1\) as a prerequisite.

Now how many different curricula are possible?

\[ \small{ \begin{aligned} B =\;& (A_1 \cap B) \cup (A_2 \cap B) \cup \cdots \cup (A_n \cap B) \\ \\ \text{P}(B) =\;& \text{P}\big((A_1 \cap B) \cup (A_2 \cap B) \cup \cdots \cup (A_n \cap B)\big)\\ =\;& \text{P}(A_1 \cap B) + \text{P}(A_2 \cap B) + \cdots + \text{P}(A_n \cap B)\\ =\;& \text{P}(A_1)\text{P}(B \mid A_1) + \text{P}(A_2)\text{P}(B \mid A_2) + \cdots + \text{P}(A_n)\text{P}(B \mid A_n) \\ \end{aligned} } \]

Divide and conquer

Exercise

You enter a tennis tournament.

Your probability of winning a game is

• 0.3 against a stronger player (half of the field)
• 0.5 against a similar-level player (a quarter of the field)
• 0.6 against a weaker player (a quarter of the field)

You play a game against a randomly chosen opponent.

What is the probability of you winning the game?

The Monty Hall problem

Assumptions

• Monty knows which room has the car.
• He always opens one of the two unchosen doors that does not have the car.
• If both unchosen doors do not have the car (i.e., your first choice is correct), Monty opens one of the two doors at random.
• You want the car, not the goat 🐐.

Simulating a single game

def monty(switch=False):
  # Generate a random door number that has the car
  import random
  car_door = random.randint(1, 3) 

  # Get keyboard input for a player's initial pick
  init_pick = int(input('Which door would you pick?'))
  
  if switch:
    if init_pick == car_door:
      print(f'You lose! The car is behind door {car_door} but you switched.')
    else:
      print(f'You win! You switched to door {car_door} which has the car.')
  else:
    if init_pick == car_door:
      print(f'You win! The car is indeed behind door {car_door}.')
    else:
      print(f'You lose! The car is behind door {car_door}')