2.6 Combination

How many ways to choose 2 students from 5 to volunteer this weekend?

Combinations - an unordered subset

How many ways to choose 3 students from 40 to form a committee.

• How many ordered list of 3 students can be formed?
• How many ways to order each chosen 3 students?

• How many ordered list of 3 students can be formed? \[3\text{-permutations of }40=\frac{40!}{(40-3)!}=59,280\]

• How many ways to order each chosen 3 students? \[\text{Permutations of }3=3!=6\]

They are: (A-B-C), (A-C-B), (B-A-C), (B-C-A), (C-A-B), (C-B-A)

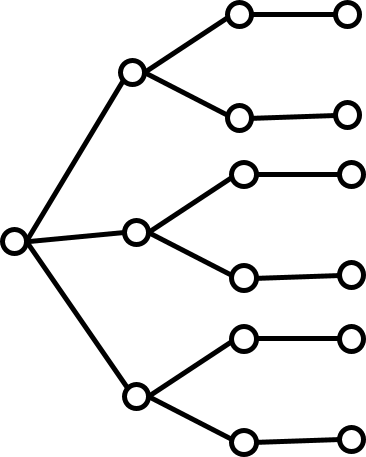
Combinations - an unordered subset

How many ways to choose 3 students from 40 to form a committee.

\[\begin{aligned} \text{number of unordered list}&=\frac{3\text{-permutations of }40}{\text{permutations of }3} \\ \\ &=\frac{40!}{3!(40-3)!} \\ \\ &=9,880 \end{aligned}\]

General formula for combinations

The number of ways of choosing \(k\) objects out of \(n\) is

\[\begin{aligned} {n \choose k}&=\frac{k\text{-permutations of }n}{\text{permutations of }k} \\ \\ &=\frac{n!}{k!(n-k)!} \\ \end{aligned}\]

Permutation vs. combination

2-permutations of 4 letters A, B, C, and D

\[\frac{4!}{(4-2)!}=12\]

AB BA AC CA AD DA BC CB BD DB CD DC

AB AC AD BC BD CD

Combinations of choosing 2 letters from 4

\[{4 \choose 2}=\frac{4!}{2!(4-2)!}=6\]

Properties

\[{n \choose k}={n \choose n-k}\]

\[{5 \choose 3}={5 \choose 5-3}\]

\[{n \choose k}={n \choose n-k}\]

Proof:

Exercise

• In a round-robin tennis tournament with \(n\) players, each player meets every other player exact once.
• How many games need to be played in total?

Powerball

• Draw five numbers from a pool of 69 white balls and one number from a pool of 26 Powerballs.
• To win a jackpot one needs to match all five white balls plus the power ball.
• What is the winning chance if you buy a single ticket?

Exercise

Toss a fair coin \(n\) times.

What is the chance there are \(k\; (= 0, 1, \cdots, n)\) heads?

Exercise

• A jar contains \(m\) maize and \(n\) blue balls.
• Two balls are drawn randomly from the jar.
• What is the chance that the balls are of the same color?

Exercise

Draw 7 cards from a well-shuffled 52-card deck.

Find the probability that

• the 7 cards include exact 3 aces
• the 7 cards include exact 2 kings
• the 7 cards include exact 3 aces or exact 2 kings

Birthday problem

How many people would it take to have a 50-50 chance that at least two of them share the same birthday?

Birthday problem

Another way to describe it:

There are \(n\) people at a party.

How likely at least two of them share their birthday?

Assumptions

• Everyone has an equal probability of being born on any day in the year, independent of everyone else.
• Ignore February 29th from leap years.

\[ \text{P(sharing birthday)}=1-\frac{365!}{(365-n)!\cdot 365^n} \]

Go to Google Colab, sign in, and open a new notebook.

from math import factorial

n = 40  # number of people at a party

p = 1 - factorial(365) / factorial(365-n) / (365**n)

print(p)

Birthday attack

Birthday problem

You walked into a party with \(n\) people.

How likely someone shares the birthday with you?