2.4 Product rule
Discrete probability law
If the sample space \(\Omega\) consists of a finite number of possible outcomes,
then the probability of any event \(\{s_1, s_2, \cdots, s_k \}\)
is the sum of the probabilities of its elements.
\[\text{P}(\{s_1, s_2, \cdots, s_k \}) = \text{P}(s_1) + \text{P}(s_2) + \cdots + \text{P}(s_k) \]
Discrete uniform probability law
If all outcomes in the sample space \(\Omega\) are equally likely,
then the probability of any event A is given by:
\[ \text{P}(A) = \frac{\text{number of outcomes in } A}{\text{number of outcomes in } \Omega} \]
For convenience, we use \(|A|\) to denote the number of elements in set \(A\) (termed the cardinality of set \(A\))
\[ \text{P}(A) = \frac{|A|}{|\Omega|} \]
Equally likely outcomes
In many experiments, it is reasonable to assume equal probabilities to all simple events.
Roll a fair six-sided die 🎲
\[ \text{P}(⚀) = \text{P}(⚁) = \text{P}(⚂) = \text{P}(⚃) = \text{P}(⚄) = \text{P}(⚅) = \frac{1}{6} \]
\[\text{P}(\text{odd number})=\text{P}\big(\{⚀, ⚂, ⚄\}\big)=\frac{3}{6}\]
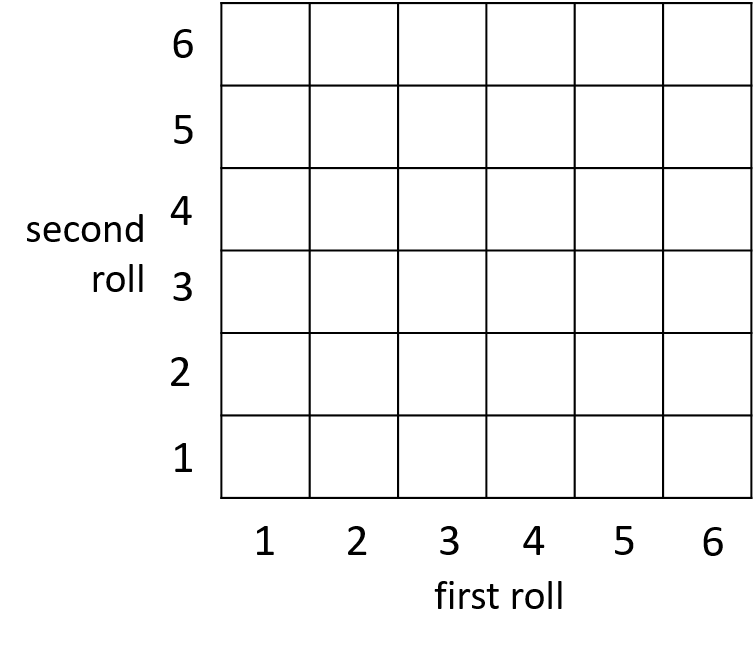
Roll two dice 🎲 🎲
- What is the probability to roll a double?
- What is the probability that the total is over 7?
Draw a card from a well-shuffled deck of 52 cards.
What is the chance to draw an ace?

\[ \text{P}(\text{Aces}) = \text{P}(\{🃑, 🃁, 🂱, 🂡\}) = \frac{4}{52}= \frac{1}{13} \]
Draw a card from a well-shuffled deck of 52 cards.
What is the chance to draw a spade?

\[ \text{P}(\text{spades}) = \text{P}(\{🂡, 🂢, \cdots, 🂮\})= \frac{13}{52}= \frac{1}{4} \]
Roll a die twice. How many pairs of numbers are possible?

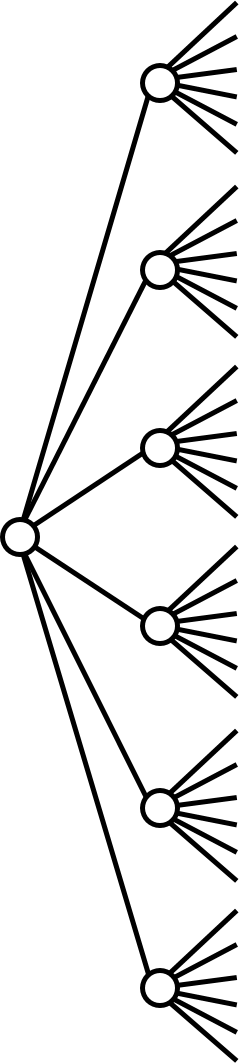
The product rule
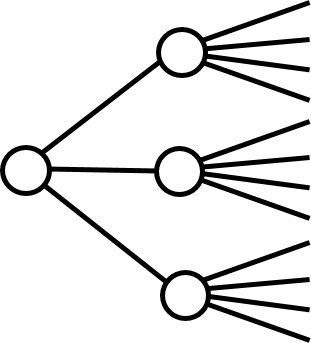
Suppose that
- there are \(\color{red}{n_1}\) possible results at the first stage
- for every possible result at the first stage, there are \(\color{green}{n_2}\) possible results at the second stage
Then the total number of possible results is \(\color{red}{n_1} \times \color{green}{n_2}\)
The product rule: four stages
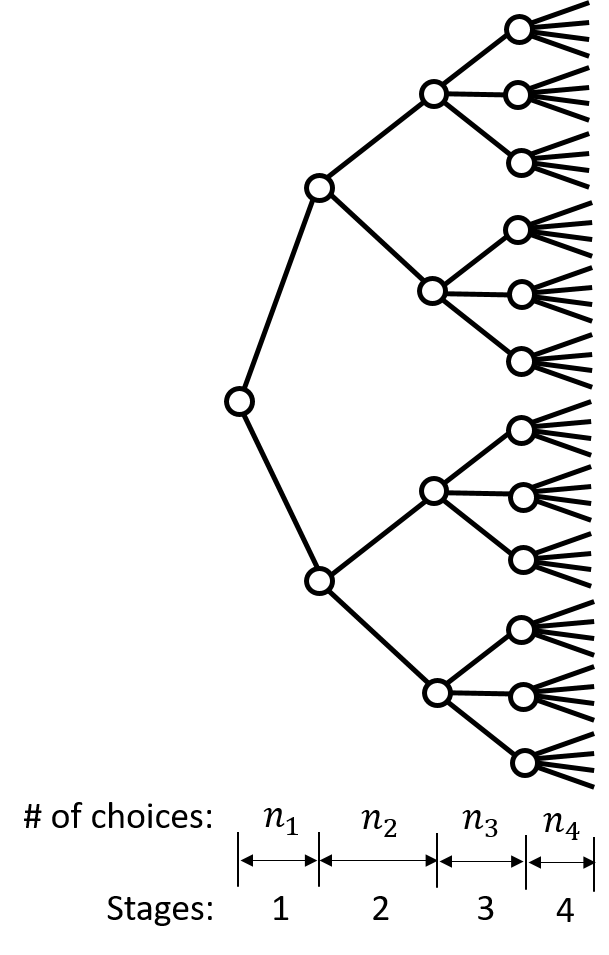
General form of the product rule with \(r\)-stages
If for any sequence of possible results at the first \((i-1)\) stages, there are \(n_i\) possible results at the \(i\)-th stage
then the total number of possible results in a \(r\)-stage process is
\[n_1 \times n_2 \times \cdots \times n_r\]
Exercise
How many iPad Pro variants does Apple need to make?
- Screen size: 11-inch, 13-inch
- Color: Space gray, Silver
- Storage: 256GB, 512GB, 1TB, 2TB
- Display glass: Standard, Nano-texture
- Connectivity: Wi-Fi, Wi-Fi + Cellular
Exercise
How many unique MI license plate numbers are there?

Rules
- 7 characters
- Only uppercase letters (A-Z) and numbers (0-9)
- Letter O is not allowed.
- Spaces are allowed and counted as characters.
Exercise
How many subsets does a \(n\)-element set have?
\[ \{s_1, s_2, \cdots, s_n\} \]