2.1 Sample space, events

Sample space

Probability starts with a sample space, which is a set that describes all possible outcomes in an experiment.

It must be collectively exhaustive & mutually exclusive.

• Flip a coin once 🪙

\[\Omega = \{\text{heads (H), tails (T)}\}\]

• Flip a coin twice 🪙 🪙

\[\Omega = \{(\text{H, H}), (\text{H, T}), (\text{T, H}), (\text{T, T})\}\]

• Roll a six-sided die once 🎲

\[\Omega = \{ ⚀, ⚁, ⚂, ⚃, ⚄, ⚅ \}\]

• Roll a six-sided die twice 🎲 🎲

\[ \begin{aligned} \Omega = \{&⚀⚀, ⚀⚁, ⚀⚂, ⚀⚃, ⚀⚄, ⚀⚅, \\ &⚁⚀, ⚁⚁, ⚁⚂, ⚁⚃, ⚁⚄, ⚁⚅, \\ &⚂⚀, ⚂⚁, ⚂⚂, ⚂⚃, ⚂⚄, ⚂⚅, \\ &⚃⚀, ⚃⚁, ⚃⚂, ⚃⚃, ⚃⚄, ⚃⚅, \\ &⚄⚀, ⚄⚁, ⚄⚂, ⚄⚃, ⚄⚄, ⚄⚅, \\ &⚅⚀, ⚅⚁, ⚅⚂, ⚅⚃, ⚅⚄, ⚅⚅ \} \end{aligned} \]

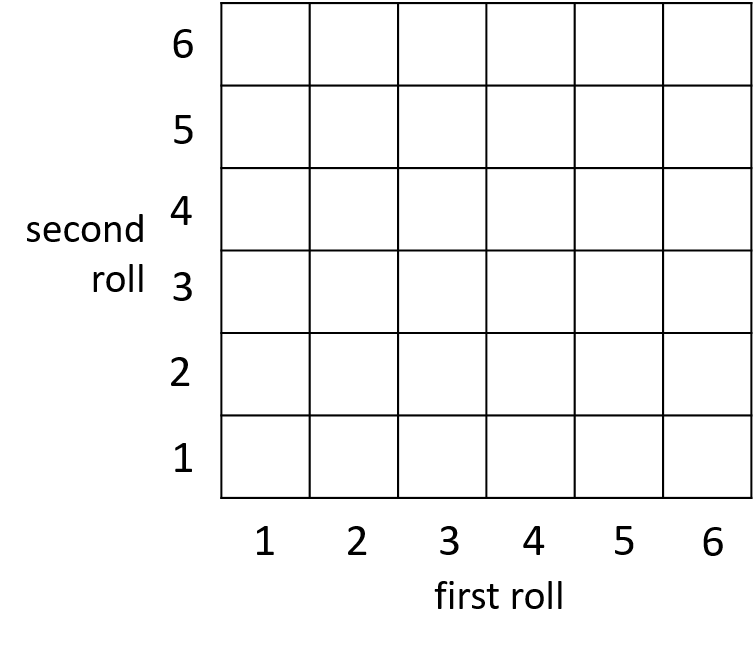
Exercise

We bet on the total from a roll of two dice 🎲 🎲

What is the sample space?

Event

A collection of outcomes in the sample space

Or simply, a subset of the sample space.

• Event A: Roll a die 🎲, it lands on an odd number.

\[A = \{ ⚀, ⚂, ⚄ \}\]

• Event B: Roll two dice 🎲 🎲, the total is under 7.

\[B = \{ 2, 3, 4, 5, 6\}\]

Event

• Event C: Making at least one basketball free throw out of two \[C=\{(\text{hit, hit}), (\text{hit, miss}), (\text{miss, hit})\}\]

Simple & compound event

A simple event consists of a single outcome.

A compound event consists of multiple outcomes.

• Roll a die 🎲, it lands on an odd number.

\[\{ ⚀, ⚂, ⚄ \}\]

• Roll two dice 🎲 🎲 and get a double.

\[\{(⚀,⚀), (⚁, ⚁), (⚂, ⚂), (⚃, ⚃), (⚄, ⚄), (⚅, ⚅) \}\]

• Roll two dice 🎲 🎲, the total is 12.

\[\{ (⚅, ⚅) \}\]

• A basketball player makes both free throws

\[\{(\text{hit, hit})\}\]

• Making at least one free throw

\[\{(\text{hit, hit}), (\text{hit, miss}), (\text{miss, hit})\}\]