1.6 Measures of variability
Measures of variability (or spread)
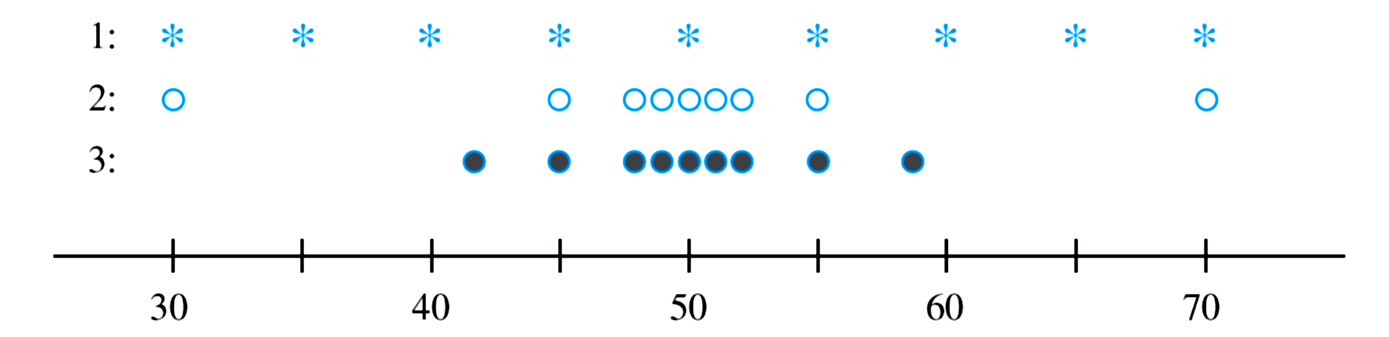
- The measures of center gives only partial information about the data.
- Different data may have similar measures of center yet differ from one another in other important ways.
Measures of variability (or spread)

How about using the range to measure the variability?
\[ \text{range} = \text{maximum value} - \text{minimum value}\]
Range is sensitive to outliers.
Measures of variability (or spread)
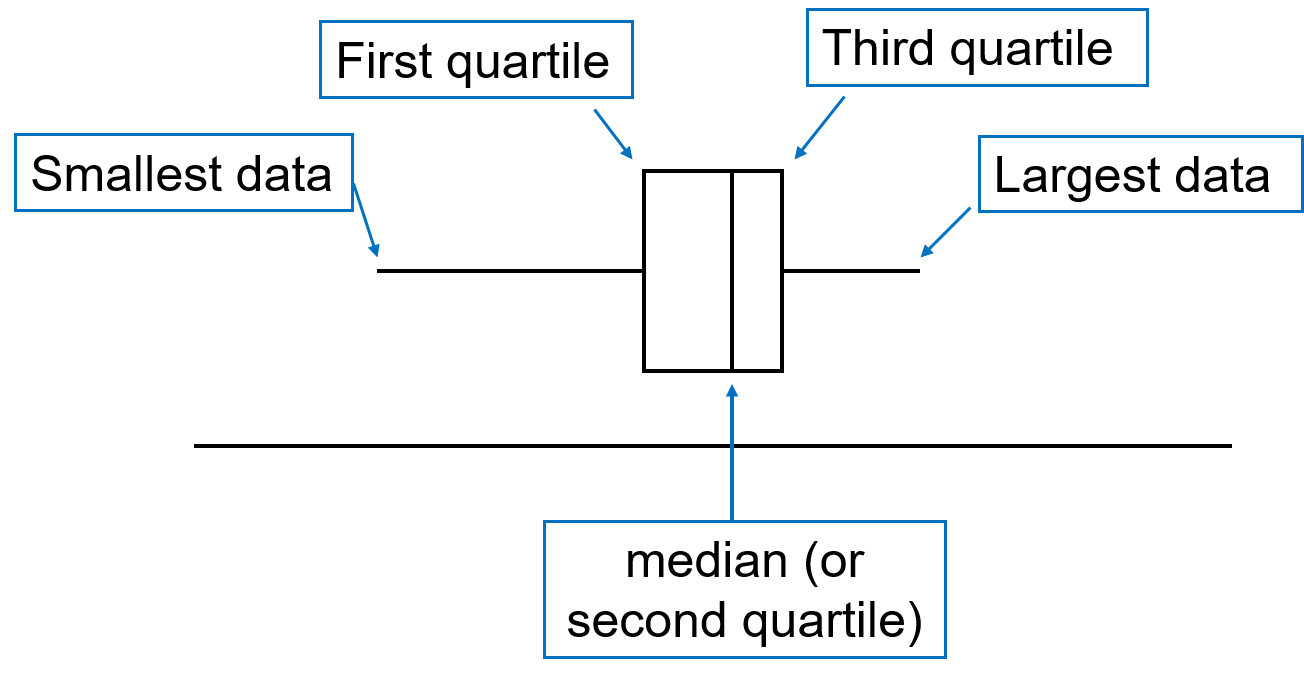
\[ \text{IQR} = \text{Third quartile} - \text{First quartile}\]
Measures of variability (or spread)
How about measuring the deviations from the sample mean?

\[x_1-\bar{x}, \;x_2-\bar{x}, \;\cdots, \;x_n-\bar{x}\]
Then, how about using the average deviation as a metric?
\[\frac{1}{n}\big[(x_1-\bar{x}) + (x_2-\bar{x}) + \cdots + (x_n-\bar{x})\big]\]
Bad idea.
We can show that the sum of all deviations from the sample mean is always zero.
\[(x_1-\bar{x}) + (x_2-\bar{x}) + \cdots + (x_n-\bar{x})=0\]
Or, \[\sum_{i=1}^{n}(x_i-\bar{x})=0\]
If we cannot use the average deviation as a metric for variability, what can we do then?
One solution is to use the absolute deviations. \[\frac{1}{n}\bigg[|x_1-\bar{x}| + |x_2-\bar{x}| + \cdots + |x_n-\bar{x}|\bigg]\]
However, absolute values would lead to a number of mathematical difficulties later on.
The squared deviations is the preferred approach. \[(x_1-\bar{x})^2, \;(x_2-\bar{x})^2, \;\cdots, \;(x_n-\bar{x})^2\]
Sample variance
\[\begin{aligned} s^2 &= \frac{(x_1-\bar{x})^2 + (x_2-\bar{x})^2 + \cdots + (x_n-\bar{x})^2}{n-1} \\\ \\\ &= \frac{\displaystyle\sum_{i=1}^{n}(x_i-\bar{x})^2}{n-1} \end{aligned}\]
Why divided by \((n-1)\) instead of \(n\)?
- Degree of freedom: The number of values in a calculation that are free to vary.
- Pick any three numbers and calculate the mean.
- Now we add some constraints:
- The numbers have to add up to 20.
- The first two numbers have to add up to 10.
\[s^2 = \frac{(x_1-\bar{x})^2 + (x_2-\bar{x})^2 + \cdots + (x_n-\bar{x})^2}{n-1}\]
Are there any constraints when we calculate the sample variance?
Example:
| \(x_i\) | \(x_i-\bar{x}\) | \((x_i-\bar{x})^2\) |
|---|---|---|
| \(9\) | ||
| \(4\) | ||
| \(5\) |
Heights (in feet) of 216 volcanoes:
\[19882, 19728, 19335, 19287, \cdots, 617, 555, 529, 242\]
Sample mean:
\[\bar{x}=7047.6 \text{ feet}\]
Sample variance:
\[s^2 = \frac{\sum_{i=1}^{n}(x_i-\bar{x})^2}{n-1}=18,507,834 \text{ feet}^2\]
\[s^2 = \frac{\sum_{i=1}^{n}(x_i-\bar{x})^2}{n-1}=18,507,834 \text{ feet}^2\]
The sample standard deviation \(s\), is given by
\[ s = \sqrt{s^2} = \sqrt{\frac{\sum_{i=1}^{n}(x_i-\bar{x})^2}{n-1}}=4302.1 \text{ (ft})\]
Property I
\(x_1, x_2, \cdots, x_n\) are sample data. \(c\) is any constant.
\[\text{If }\; y_1=x_1+c, \;y_2=x_2+c, \;\cdots, \;y_n=x_n+c\]
\[\begin{aligned} \text{then }\; s_y^2&=s_x^2 \\\ (\text{or }s_y&=s_x) \end{aligned}\]
Intuition: Adding a constant to the data shifts the distribution right or left without changing its shape, and thus its spread.
Property II
\(x_1, x_2, \cdots, x_n\) are sample data and \(c\) is any constant.
\[\text{If }\; y_1=cx_1, \;y_2=cx_2, \;\cdots, \;y_n=cx_n\]
\[\begin{aligned} \text{then } \; s_y^2&=c^2s_x^2 \\\ (\text{or }s_y&=cs_x) \end{aligned}\]
Intuition: Multiplying a constant to the data changes its shape, and thus its spread.
Descriptive statistics with Python
Go to Google Colab and sign in. Open a new notebook.
ages = [12, 34, 14, 5, 44, 28, 22, 19, 36, 25]
mean = sum(ages) / len(ages)
squared_dev = [(x-mean)**2 for x in ages]
var = sum(squared_dev) / (len(ages) - 1)
print(var)
print(var**0.5)Descriptive statistics with Python
We use the pandas library.
import pandas
url = "https://imse317.github.io/lecture-slides/ch01/data/bank.csv"
bank = pandas.read_csv(url)
bank.head()