1.5 Measures of location

Heights (in feet) of 216 volcanoes


\[19882, 19728, 19335, 19287, \cdots, 617, 555, 529, 242\]

volcano-heights.csv


What is the typical height of a volcano?

Descriptive statistics

Describe & summarize important features of the data.

  • Numerical methods
    • Measures of location (i.e., center)
    • Measures of variability (i.e., spread)
  • Graphical methods
    • Histogram
    • Boxplot

Measures of location

  • Sample mean
  • Sample median
  • Quartile/percentile
  • Trimmed mean
  • Boxplot

Sample mean

For a given set of \(n\) numbers

\[x_1, x_2, \cdots, x_n\]

the sample mean \(\bar{x}\) is given by

\[\bar{x} = \frac{1}{n}(x_1 + x_2 + \cdots + x_n)\]

We often use the shorthand sigma notation

\[\bar{x} = \frac{1}{n}\sum_{i=1}^n x_i\]

Sample mean

\[12, 34, 14, 5, 44, 28, 22, 19, 36, 25\]

\[\bar{x} = \frac{1}{10}(12 + 34 + \cdots + 25)=23.9\]

Interpretation: the center of gravity for a series of weights positioned at the specified values in a dot plot.

  • In a startup company of 10 people
  • 9 employees earn a salary of $50k a year each
  • The CEO earns $550k a year

\[50, 50, 50, 50, 50, 50, 50, 50, 50, 550\]

\[\bar{x} = \frac{1}{10}(50\times9 + 550\times1)=100\]

  • One may argue that $100k is not a “typical” value.

\[50, 50, 50, 50, 50, 50, 50, 50, 50, 550\]


Sample mean is sensitive to the presence of outliers1, especially for small data sets.

Sample median

The median, \(\tilde{x}\) (reads x tilde), is the middle value in a set of data that is arranged in order.

If the sample size \(n\) is an even number, there are two middle values.

\[1, 3, 4, 6, 8, 9\]

\(\tilde{x}\) is the average of the two.

Exercise

Data set:

\[12, 34, 14, 5, 44, 28, 22, 19, 36, 25\]

Sort the data to order:

\[5, 12, 14, 19, 22, 25, 28, 34, 36, 44\]

\[\tilde{x} = \frac{1}{2}(22+25)=23.5\]

Interpretation: half of the data are smaller than 23.5, half are larger than 23.5.

The earlier startup company example

\[50, 50, 50, 50, 50, 50, 50, 50, 50, 550\]

\[\tilde{x} = \frac{1}{2}(50 + 50)=50\]

  • The median of $50k is arguably more “typical”.
  • The median is less sensitive to outliers.

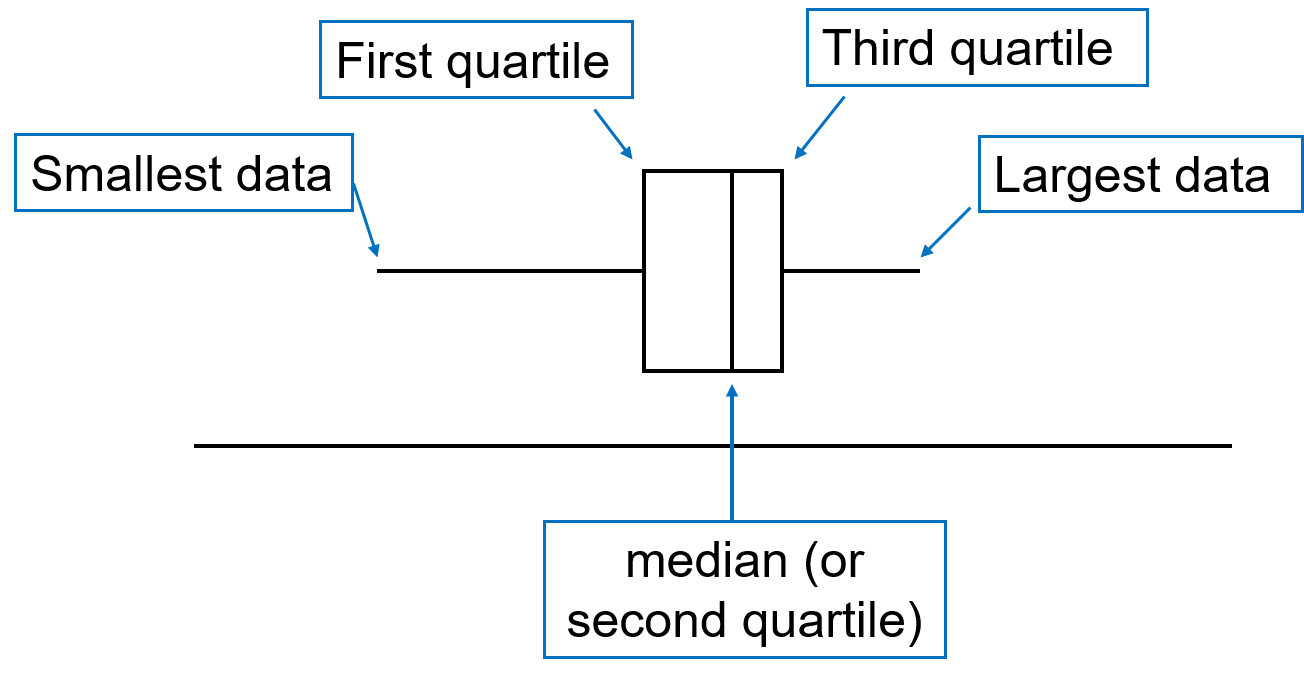
Quartiles & percentiles

  • First quartile (25th percentile)
    • Separating the bottom 25% data from the top 75%
    • The middle value between the smallest and median.
  • Second quartile (50th percentile, or simply, the median)
    • Separating the bottom 50% data from the top 50%
  • Third quartile (75th percentile)
    • Separating the bottom 75% data from the top 25%
    • The middle value between the median and largest.

\(x\text{-th}\) percentile

The value below which \(x\%\) of the data will be found.

Image source

\[\text{Percentile} = \frac{r-0.5}{n}\times100\]

\(\text{Rank }(r)\)   \(x_i\)    \(\text{Percentile}\) 
\(1\) \(5\) \(5\text{th}\)
\(2\) \(12\) \(15\text{th}\)
\(3\) \(14\) \(25\text{th}\)
\(\cdots\) \(\cdots\) \(\cdots\)
\(8\) \(34\) \(75\text{th}\)
\(9\) \(36\) \(85\text{th}\)
\(10\) \(44\) \(95\text{th}\)

Trimmed mean

The mean after discarding the smallest & largest \(\alpha\%\) of the data

Dive scores from 7 judges:

\[4, 6, 6, 6, 7, 7, 8\]

The lowest and highest scores are eliminated.

\[6, 6, 6, 7, 7\]

The remaining scores are totaled.

\[6+6+6+7+7=32\]

Trimmed mean

Typically \(\alpha\%\) is between 5 to 25%.

When discarding the bottom 25% and top 25%, it is called the interquartile mean.


The sample mean and median can be considered as two special cases of trimmed mean.

  • \(\alpha\%=0\%\)
    • Discard no data: mean
  • \(\alpha\%=50\%\)
    • Discard all but the middle number(s): median

A simple boxplot


How much space does drivers give to cyclists when passing?

Descriptive statistics with Python

Go to Google Colab and sign in. Open a new notebook.


ages = [12, 34, 14, 5, 44, 28, 22, 19, 36, 25]

print(sum(ages)/len(ages))

import statistics
print(statistics.mean(ages))
print(statistics.median(ages))
print(statistics.quantiles(ages))

Descriptive statistics with Python

bank.csv

We use the pandas library.


import pandas
url = "https://imse317.github.io/lecture-slides/ch01/data/bank.csv"
bank = pandas.read_csv(url)
bank.head()


bank.describe()
bank['age'].mean()
bank['age'].median()
bank['age'].quantile(0.99)